题目内容
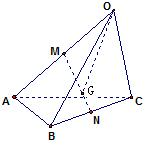
已知空间四边形OABC,其对角线是OB,AC,M,N分别是对边OA,BC的中点,点G在线段MN上,且MG=3GN,用基底向量
,
,
表示向量
应是( )
| OA |
| OB |
| OC |
| OG |
A.
| B.
| ||||||||||||||||||||||||||||
C.
| D.
|
∵
=
+
=
+
=
+
(
+
+
)
=
+
+
+
×
=
+
+
(
-
)
=
+
+
故选A.
| OG |
| OM |
| MG |
| OM |
| 3 |
| 4 |
| MN |
| OM |
| 3 |
| 4 |
| MO |
| OC |
| CN |
=
| OM |
| 3 |
| 4 |
| MO |
| 3 |
| 4 |
| OC |
| 3 |
| 4 |
| 1 |
| 2 |
| CB |
=
| 1 |
| 4 |
| OM |
| 3 |
| 4 |
| OC |
| 3 |
| 8 |
| OB |
| OC |
=
| 1 |
| 8 |
| OA |
| 3 |
| 8 |
| OB |
| 3 |
| 8 |
| OC |
故选A.


练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
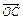 =
=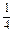
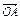 ,
,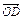 =
=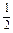
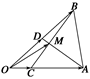
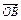 ,AD与BC相交于点M,设
,AD与BC相交于点M,设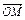 .
.
 为
为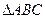 的外心,以线段
的外心,以线段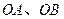 为邻边作平行四边形,第四个顶点为
为邻边作平行四边形,第四个顶点为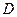 ,再以
,再以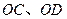 为邻边作平行四边形,它的第四个顶点为
为邻边作平行四边形,它的第四个顶点为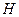 .
.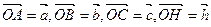 ,试用
,试用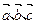 表示
表示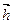 ; (2)证明:
; (2)证明: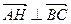 ;
;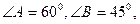 外接圆的半径为
外接圆的半径为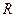 ,用
,用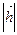 .
.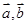 满足:
满足: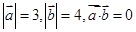 .以
.以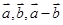 的模为边长构成三角形,则它的边与半径为
的模为边长构成三角形,则它的边与半径为 的圆的公共点个数最多为 ( )
的圆的公共点个数最多为 ( )

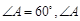 的平分线交BC于D,AB="4,"
的平分线交BC于D,AB="4," 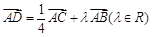 ,则AD的长为( )
,则AD的长为( )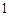
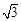
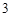
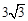
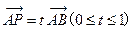 ,则
,则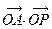 的最大值是 ( )
的最大值是 ( )
 D.3a
D.3a