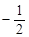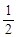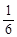题目内容
设A，B，C为单位圆O上不同的三点，则点集A={(x，y)|
=x
+y
，0＜x＜2，0＜y＜2}所对应的平面区域的面积为（ ）
| OC |
| OA |
| OB |
| A．1 | B．
| C．2 | D．
|
将
=x
+y
两边平方得：
2=x2
2+y2
2+2xy
•
cos∠AOB．
∵|
|=|
|=|
|=1，
∴1=x2+y2+2xycos∠AOB，
∵0＜x＜2，0＜y＜2．
从而由余弦定理可知x、y、1可以构成三角形，且∠AOB不是0°或180°．
于是有：
，化为
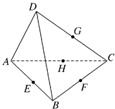
画出平面区域，结合图形可知约束条件表示的图形为阴影区域内，
∴表示的平面区域的面积是4-3×
=
．
故答案为：
．
| OC |
| OA |
| OB |
| OC |
| OA |
| OB |
| OA |
| OB |
∵|
| OA |
| OB |
| OC |
∴1=x2+y2+2xycos∠AOB，
∵0＜x＜2，0＜y＜2．
从而由余弦定理可知x、y、1可以构成三角形，且∠AOB不是0°或180°．
于是有：
|
|
画出平面区域，结合图形可知约束条件表示的图形为阴影区域内，
∴表示的平面区域的面积是4-3×
| 1 |
| 2 |
| 5 |
| 2 |
故答案为：
| 5 |
| 2 |
练习册系列答案
普通高中同步练习册系列答案
优翼小帮手同步口算系列答案
相关题目
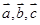为非零向量，已知向量
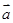与
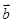不共线，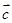
共线，则向量
与
的夹角是
，且
，则
( )．
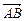=a+2b，
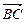=－4a－b，
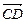=－5a－3b，其中a、b不共线，则四边形ABCD为（ ）
，
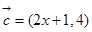，若
，则实数
的值等于（ ）
