题目内容
在平面直角坐标系xOy中,直线l:x-y+3=0与圆O:x2+y2=r2(r>0)相交于A,B两点.若
+2
=
,且点C也在圆O上,则圆O的半径r=______.
| OA |
| OB |
| 3 |
| OC |
设点A(x1,y1),B(x2,y2).
联立x-y+3=0与圆O:x2+y2=r2(r>0)
,消去y得到关于x的一元二次方程2x2+6x+9-r2=0,
∵直线l与圆O相较于A、B两点,则△=36-8(9-r2)>0.(*)
∴x1+x2=-3,x1•x2=
.
设点C(x0,y0).
∵
+2
=
,且点C也在圆O上,
(x1,y1,)+2(x2,y2)=
(x0,y0).
又∵y1=x1+3,y2=x2+3.
∴可得:
代入圆O的方程得(
)2+(
)2=r2,
化为(x1+2x2)2+(x1+2x2+9)2=3r2,
再与x1+x2=-3,x1•x2=
联立
消去x1,x2化为r2=18,满足(*).
故答案为:3
联立x-y+3=0与圆O:x2+y2=r2(r>0)
,消去y得到关于x的一元二次方程2x2+6x+9-r2=0,
∵直线l与圆O相较于A、B两点,则△=36-8(9-r2)>0.(*)
∴x1+x2=-3,x1•x2=
| 9-r2 |
| 2 |
设点C(x0,y0).
∵
| OA |
| OB |
| 3 |
| OC |
(x1,y1,)+2(x2,y2)=
| 3 |
又∵y1=x1+3,y2=x2+3.
∴可得:
|
代入圆O的方程得(
| x1+2x2 | ||
|
| x1+2x2+9 | ||
|
化为(x1+2x2)2+(x1+2x2+9)2=3r2,
再与x1+x2=-3,x1•x2=
| 9-r2 |
| 2 |
消去x1,x2化为r2=18,满足(*).
故答案为:3
| 2 |

练习册系列答案
相关题目
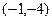 ,B(5,2),线段AB上的三等分点依次为
,B(5,2),线段AB上的三等分点依次为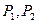 ,求
,求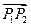 所成的比.
所成的比.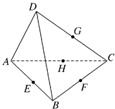
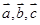 为非零向量,已知向量
为非零向量,已知向量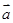 与
与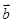 不共线,
不共线,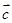 共线,则向量
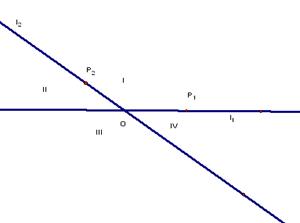
共线,则向量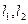 将平面分割成
将平面分割成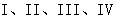 四个区域(不包含边界),向量
四个区域(不包含边界),向量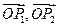 分别为
分别为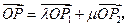 且点P落在第
且点P落在第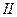 区域,则实数
区域,则实数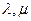 满足
满足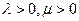
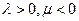
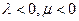
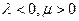
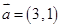 ,
,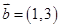 ,
, ,若
,若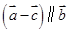 ,则k =( )
,则k =( )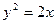 与过焦点的直线交于A,B两点,则
与过焦点的直线交于A,B两点,则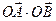 的值为________
的值为________