题目内容
已知直线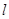 过点
过点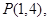
(1)若直线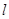 在坐标轴上的截距相等,求直线
在坐标轴上的截距相等,求直线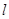 的方程;
的方程;
(2)若直线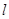 与坐标轴的正半轴相交,求使直线
与坐标轴的正半轴相交,求使直线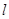 在两坐标轴上的截距之和最小时,直线
在两坐标轴上的截距之和最小时,直线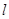 的方程。
的方程。
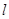 过点
过点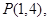
(1)若直线
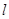 在坐标轴上的截距相等,求直线
在坐标轴上的截距相等,求直线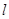 的方程;
的方程;(2)若直线
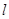 与坐标轴的正半轴相交,求使直线
与坐标轴的正半轴相交,求使直线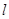 在两坐标轴上的截距之和最小时,直线
在两坐标轴上的截距之和最小时,直线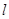 的方程。
的方程。(1)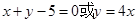 (2)
(2)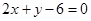
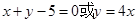 (2)
(2)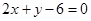
试题分析:(1)当截距为零时直线为
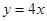 ,当截距不为零时,设直线为
,当截距不为零时,设直线为 ,代入点
,代入点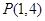 得
得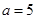 ,所以直线为
,所以直线为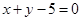 4分
4分(2)
 设所求直线L的方程为:
设所求直线L的方程为: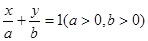
∵直线L经过点P(1,4) ∴

 8分
8分∴
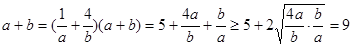 12分
12分当且仅当

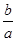 即
即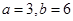 时
时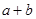 有最小値为9,
有最小値为9,所求直线方程为
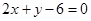 。 14分
。 14分点评:第一问中截距相等要分截距为零与不为零两种情况,第二问中求截距之和的最小值用到了均值不等式,但要注意验证等号成立条件

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
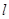 经过两点P1(4,-2)和P2(-1,8)。
经过两点P1(4,-2)和P2(-1,8)。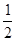

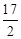
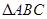 中,
中,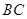 边上的高所在的直线的方程为
边上的高所在的直线的方程为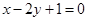 ,
,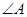 的平分线所在直线的方程为
的平分线所在直线的方程为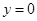 ,若点
,若点 的坐标为
的坐标为 。
。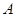 的坐标;
的坐标;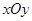 内,已知点
内,已知点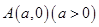 ,点
,点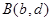 在函数
在函数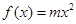
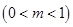 的图象上,
的图象上,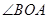 的平分线与
的平分线与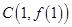 ,则实数
,则实数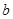 的取值范围是( ).
的取值范围是( ).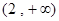

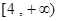

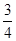 ,且与坐标轴所围成的三角形的周长是12的直线的方程。
,且与坐标轴所围成的三角形的周长是12的直线的方程。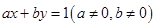 与圆
与圆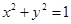 相切,若
相切,若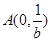 ,
,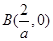 ,则
,则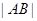 的最小值为 .
的最小值为 .