题目内容
已知点B是半圆x2+y2=1（y＞0）上的一个动点，点A的坐标为（2，0），△ABC是以BC为斜边的等腰直角三角形，且顶点A、B、C按顺时针方向排列．求点C的轨方程．
设C（x，y），令B（x0，y0），
∵点A的坐标为（2，0），△ABC是以BC为斜边的等腰直角三角形，
∴kAB×kAC=-1，且AB=AC
∴
×
=-1 ①；
（x-2）2+y2=（x0-2）2+y02 ②
由①得x0-2=
代入②得（x-2）2+y2=(
)2+y0 2
整理得（x-2）2+y2=y0 2×(1+
)，即y0 2=
=（x-2）2
又y0＞0，x≥2
可得y0=x-2代入①得
=-1，解得x0=2-y
又点B（x0，y0）是半圆x2+y2=1（y＞0）上的一个动点
所以有（x-2）2+（y-2）2=1（x≥2）
故点C的轨迹方程是（x-2）2+（y-2）2=1（x≥2）
∵点A的坐标为（2，0），△ABC是以BC为斜边的等腰直角三角形，
∴kAB×kAC=-1，且AB=AC
∴
| y |
| x-2 |
| y0 |
| x0-2 |
（x-2）2+y2=（x0-2）2+y02 ②
由①得x0-2=
| yy0 |
| x-2 |
| yy0 |
| x-2 |
整理得（x-2）2+y2=y0 2×(1+
| y2 |
| (x-2)2 |
| (x-2)2+y2 | ||
1+
|
又y0＞0，x≥2
可得y0=x-2代入①得
| y |
| x0-2 |
又点B（x0，y0）是半圆x2+y2=1（y＞0）上的一个动点
所以有（x-2）2+（y-2）2=1（x≥2）
故点C的轨迹方程是（x-2）2+（y-2）2=1（x≥2）
练习册系列答案
相关题目
已知半椭圆
和半圆x2+y2=b2（y≤0）组成曲线C，其中a＞b＞0；如图，半椭圆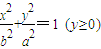
内切于矩形ABCD，且CD交y轴于点G，点P是半圆x2+y2=b2（y≤0）上异于A，B的任意一点，当点P位于点
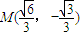时，△AGP的面积最大．