题目内容
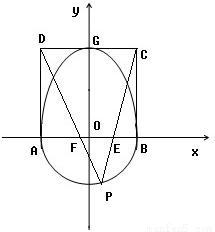
已知半椭圆 和半圆x2+y2=b2(y≤0)组成曲线C,其中a>b>0;如图,半椭圆
和半圆x2+y2=b2(y≤0)组成曲线C,其中a>b>0;如图,半椭圆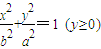 内切于矩形ABCD,且CD交y轴于点G,点P是半圆x2+y2=b2(y≤0)上异于A,B的任意一点,当点P位于点
内切于矩形ABCD,且CD交y轴于点G,点P是半圆x2+y2=b2(y≤0)上异于A,B的任意一点,当点P位于点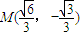 时,△AGP的面积最大.
时,△AGP的面积最大.(1)求曲线C的方程;
(2)连PC、PD交AB分别于点E、F,求证:AE2+BF2为定值.

【答案】分析:(1)由题设条件知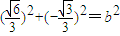 ,所以b=1,由此可知半圆x2+y2=b2(y≤0)在点M处的切线与直线AG平行,所以OM⊥AG,
,所以b=1,由此可知半圆x2+y2=b2(y≤0)在点M处的切线与直线AG平行,所以OM⊥AG,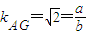 ,所以
,所以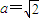 ,所以曲线C的方程为
,所以曲线C的方程为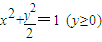 或x2+y2=1(y≤0).
或x2+y2=1(y≤0).
(2)设P(x,y),则有直线PC的方程为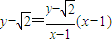 ,令y=0,得B1,所以
,令y=0,得B1,所以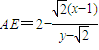 ;直线PD的方程为
;直线PD的方程为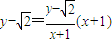 ,令y=0,得
,令y=0,得 ,
,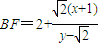 .由此入手能够推导出AE2+BF2为定值.
.由此入手能够推导出AE2+BF2为定值.
解答:解:(1)已知点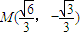
在半圆x2+y2=b2(y≤0)上,
所以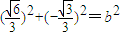 ,又b>0,
,又b>0,
所以b=1,当半圆x2+y2=b2(y≤0)
在点P处的切线与直线AG平行时,
点P到直线AG的距离最大,
此时△AGP的面积取得最大值,
故半圆x2+y2=b2(y≤0)
在点M处的切线与直线AG平行,
所以OM⊥AG,又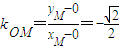 ,
,
所以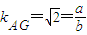 ,又b=1,所以
,又b=1,所以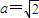 ,(4分)
,(4分)
所以曲线C的方程为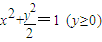 或x2+y2=1(y≤0).
或x2+y2=1(y≤0).
(2)点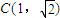 ,点
,点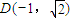 ,
,
设P(x,y),则有直线PC的方程为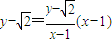 ,
,
令y=0,得x=1-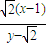 ,
,
所以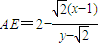 ;
;
直线PD的方程为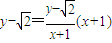 ,
,
令y=0,得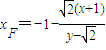 ,
,
所以 ;
;
则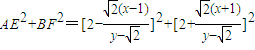
= ,
,
又由x2+y2=1,得x2=1-y2,
代入上式得AE2+BF2=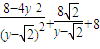
=
=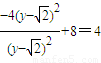 ,所以AE2+BF2为定值.
,所以AE2+BF2为定值.
点评:本题考查圆锥曲线的综合应用,解题时要认真审题,仔细解答.
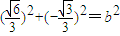 ,所以b=1,由此可知半圆x2+y2=b2(y≤0)在点M处的切线与直线AG平行,所以OM⊥AG,
,所以b=1,由此可知半圆x2+y2=b2(y≤0)在点M处的切线与直线AG平行,所以OM⊥AG,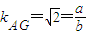 ,所以
,所以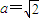 ,所以曲线C的方程为
,所以曲线C的方程为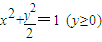 或x2+y2=1(y≤0).
或x2+y2=1(y≤0).(2)设P(x,y),则有直线PC的方程为
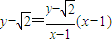 ,令y=0,得B1,所以
,令y=0,得B1,所以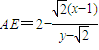 ;直线PD的方程为
;直线PD的方程为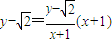 ,令y=0,得
,令y=0,得 ,
,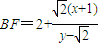 .由此入手能够推导出AE2+BF2为定值.
.由此入手能够推导出AE2+BF2为定值.解答:解:(1)已知点
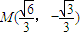
在半圆x2+y2=b2(y≤0)上,
所以
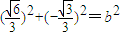 ,又b>0,
,又b>0,所以b=1,当半圆x2+y2=b2(y≤0)
在点P处的切线与直线AG平行时,
点P到直线AG的距离最大,
此时△AGP的面积取得最大值,
故半圆x2+y2=b2(y≤0)
在点M处的切线与直线AG平行,
所以OM⊥AG,又
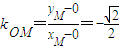 ,
,所以
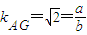 ,又b=1,所以
,又b=1,所以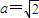 ,(4分)
,(4分)所以曲线C的方程为
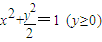 或x2+y2=1(y≤0).
或x2+y2=1(y≤0).(2)点
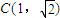 ,点
,点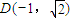 ,
,设P(x,y),则有直线PC的方程为
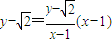 ,
,令y=0,得x=1-
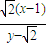 ,
,所以
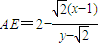 ;
;直线PD的方程为
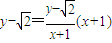 ,
,令y=0,得
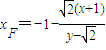 ,
,所以
 ;
;则
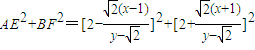
=
 ,
,又由x2+y2=1,得x2=1-y2,
代入上式得AE2+BF2=
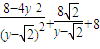
=

=
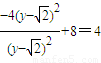 ,所以AE2+BF2为定值.
,所以AE2+BF2为定值.点评:本题考查圆锥曲线的综合应用,解题时要认真审题,仔细解答.

练习册系列答案
相关题目
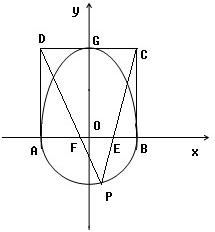 已知半椭圆
已知半椭圆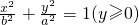 和半圆x2+y2=b2(y≤0)组成曲线C,其中a>b>0;如图,半椭圆
和半圆x2+y2=b2(y≤0)组成曲线C,其中a>b>0;如图,半椭圆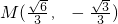 时,△AGP的面积最大.
时,△AGP的面积最大.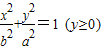 和半圆x2+y2=b2(y≤0)组成曲线C,其中a>b>0;如图,半椭圆
和半圆x2+y2=b2(y≤0)组成曲线C,其中a>b>0;如图,半椭圆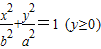 内切于矩形ABCD,且CD交y轴于点G,点P是半圆x2+y2=b2(y≤0)上异于A,B的任意一点,当点P位于点
内切于矩形ABCD,且CD交y轴于点G,点P是半圆x2+y2=b2(y≤0)上异于A,B的任意一点,当点P位于点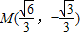 时,△AGP的面积最大.
时,△AGP的面积最大.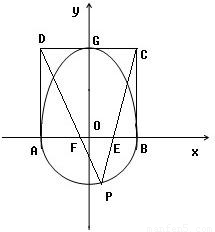
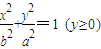 和半圆x2+y2=b2(y≤0)组成曲线C,其中a>b>0;如图,半椭圆
和半圆x2+y2=b2(y≤0)组成曲线C,其中a>b>0;如图,半椭圆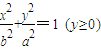 内切于矩形ABCD,且CD交y轴于点G,点P是半圆x2+y2=b2(y≤0)上异于A,B的任意一点,当点P位于点
内切于矩形ABCD,且CD交y轴于点G,点P是半圆x2+y2=b2(y≤0)上异于A,B的任意一点,当点P位于点 时,△AGP的面积最大.
时,△AGP的面积最大.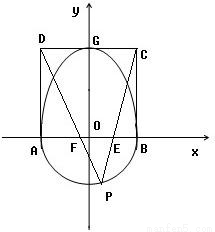
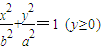 和半圆x2+y2=b2(y≤0)组成曲线C,其中a>b>0;如图,半椭圆
和半圆x2+y2=b2(y≤0)组成曲线C,其中a>b>0;如图,半椭圆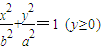 内切于矩形ABCD,且CD交y轴于点G,点P是半圆x2+y2=b2(y≤0)上异于A,B的任意一点,当点P位于点
内切于矩形ABCD,且CD交y轴于点G,点P是半圆x2+y2=b2(y≤0)上异于A,B的任意一点,当点P位于点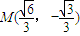 时,△AGP的面积最大.
时,△AGP的面积最大.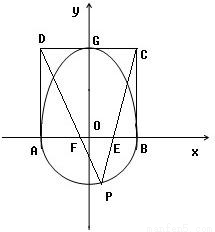
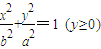 和半圆x2+y2=b2(y≤0)组成曲线C,其中a>b>0;如图,半椭圆
和半圆x2+y2=b2(y≤0)组成曲线C,其中a>b>0;如图,半椭圆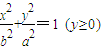 内切于矩形ABCD,且CD交y轴于点G,点P是半圆x2+y2=b2(y≤0)上异于A,B的任意一点,当点P位于点
内切于矩形ABCD,且CD交y轴于点G,点P是半圆x2+y2=b2(y≤0)上异于A,B的任意一点,当点P位于点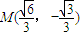 时,△AGP的面积最大.
时,△AGP的面积最大.