题目内容
 已知半椭圆
已知半椭圆| x2 |
| b2 |
| y2 |
| a2 |
| x2 |
| b2 |
| y2 |
| a2 |
| ||
| 3 |
| ||
| 3 |
(1)求曲线C的方程;
(2)连PC、PD交AB分别于点E、F,求证:AE2+BF2为定值.
分析:(1)由题设条件知(
)2+(-
)2=b2,所以b=1,由此可知半圆x2+y2=b2(y≤0)在点M处的切线与直线AG平行,所以OM⊥AG,kAG=
=
,所以a=
,所以曲线C的方程为x2+
=1 (y≥0)或x2+y2=1(y≤0).
(2)设P(x0,y0),则有直线PC的方程为y-
=
(x-1),令y=0,得B1,所以AE=2-
;直线PD的方程为y-
=
(x+1),令y=0,得xF=-1-
,BF=2+
.由此入手能够推导出AE2+BF2为定值.
| ||
| 3 |
| ||
| 3 |
| 2 |
| a |
| b |
| 2 |
| y2 |
| 2 |
(2)设P(x0,y0),则有直线PC的方程为y-
| 2 |
y0-
| ||
| x0-1 |
| ||
y0-
|
| 2 |
y0-
| ||
| x0+1 |
| ||
y0-
|
| ||
y0-
|
解答:解:(1)已知点M(
,-
)
在半圆x2+y2=b2(y≤0)上,
所以(
)2+(-
)2=b2,又b>0,
所以b=1,当半圆x2+y2=b2(y≤0)
在点P处的切线与直线AG平行时,
点P到直线AG的距离最大,
此时△AGP的面积取得最大值,
故半圆x2+y2=b2(y≤0)
在点M处的切线与直线AG平行,
所以OM⊥AG,又kOM=
=-
,
所以kAG=
=
,又b=1,所以a=
,(4分)
所以曲线C的方程为x2+
=1 (y≥0)或x2+y2=1(y≤0).
(2)点C(1,
),点D(-1,
),
设P(x0,y0),则有直线PC的方程为y-
=
(x-1),
令y=0,得x=1-
,
所以AE=2-
;
直线PD的方程为y-
=
(x+1),
令y=0,得xF=-1-
,
所以BF=2+
;
则AE2+BF2=[2-
]2+[2+
]2
=
+
+8,
又由x02+y02=1,得x02=1-y02,
代入上式得AE2+BF2=
+
+8
=
+8
=
+8=4,所以AE2+BF2为定值.
| ||
| 3 |
| ||
| 3 |
在半圆x2+y2=b2(y≤0)上,
所以(
| ||
| 3 |
| ||
| 3 |
所以b=1,当半圆x2+y2=b2(y≤0)
在点P处的切线与直线AG平行时,
点P到直线AG的距离最大,
此时△AGP的面积取得最大值,
故半圆x2+y2=b2(y≤0)
在点M处的切线与直线AG平行,
所以OM⊥AG,又kOM=
| yM-0 |
| xM-0 |
| ||
| 2 |
所以kAG=
| 2 |
| a |
| b |
| 2 |
所以曲线C的方程为x2+
| y2 |
| 2 |
(2)点C(1,
| 2 |
| 2 |
设P(x0,y0),则有直线PC的方程为y-
| 2 |
y0-
| ||
| x0-1 |
令y=0,得x=1-
| ||
y0-
|
所以AE=2-
| ||
y0-
|
直线PD的方程为y-
| 2 |
y0-
| ||
| x0+1 |
令y=0,得xF=-1-
| ||
y0-
|
所以BF=2+
| ||
y0-
|
则AE2+BF2=[2-
| ||
y0-
|
| ||
y0-
|
=
4
| ||
(y0-
|
8
| ||
y0-
|
又由x02+y02=1,得x02=1-y02,
代入上式得AE2+BF2=
8-4
| ||
(y0-
|
8
| ||
y0-
|
=
8-4
| ||||||
(y0-
|
=
-4(y0-
| ||
(y0-
|
点评:本题考查圆锥曲线的综合应用,解题时要认真审题,仔细解答.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案
相关题目
 已知半椭圆
已知半椭圆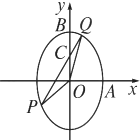 已知椭圆
已知椭圆