题目内容
已知点B是半圆x2+y2=1(y>0)上的一个动点,点A的坐标为(2,0),△ABC是以BC为斜边的等腰直角三角形,且顶点A、B、C按顺时针方向排列.求点C的轨方程.
【答案】分析:由题意“已知点B是半圆x2+y2=1(y>0)上的一个动点,点A的坐标为(2,0),△ABC是以BC为斜边的等腰直角三角形,且顶点A、B、C按顺时针方向排列.求点C的轨方程”,可设C(x,y),令B(x,y),由等腰直角三角形的特征,两直角边垂直且相等建立B,C两点的坐标之间的关系,用点C的坐标,表示出点B的坐标,代入x2+y2=1,整理即可得到点C的轨迹方程
解答:解:设C(x,y),令B(x,y),
∵点A的坐标为(2,0),△ABC是以BC为斜边的等腰直角三角形,
∴kAB×kAC=-1,且AB=AC
∴ ①;
①;
(x-2)2+y2=(x-2)2+y2 ②
由①得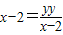 代入②得(x-2)2+y2=
代入②得(x-2)2+y2=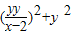
整理得(x-2)2+y2=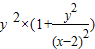 ,即
,即 =(x-2)2
=(x-2)2
又y>0,x≥2
可得y=x-2代入①得 ,解得x=2-y
,解得x=2-y
又点B(x,y)是半圆x2+y2=1(y>0)上的一个动点
所以有(x-2)2+(y-2)2=1(x≥2)
故点C的轨迹方程是(x-2)2+(y-2)2=1(x≥2)
点评:本题考查求轨迹方程,解题的关键是理解题意,建立起已知轨迹方程的曲线上的点B的坐标与要求的轨迹方程的曲线上的点C的坐标之间的关系,再代入已知的轨迹方程,整理得出要求的轨迹方程,此过程称为代入法,其步骤为未知表示已知,再代入已知得出要求的轨迹方程,本题由垂直与线段相等两个关系建立方程,由于都是符号运算,运算量较大,变形时要严谨,不要因为运算出错,导致解题失败,由解题过程可以看出,此类题求解规律固定,入手一般是从找等量关系开始,切记!
解答:解:设C(x,y),令B(x,y),
∵点A的坐标为(2,0),△ABC是以BC为斜边的等腰直角三角形,
∴kAB×kAC=-1,且AB=AC
∴
 ①;
①;(x-2)2+y2=(x-2)2+y2 ②
由①得
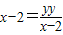 代入②得(x-2)2+y2=
代入②得(x-2)2+y2=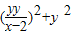
整理得(x-2)2+y2=
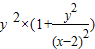 ,即
,即 =(x-2)2
=(x-2)2又y>0,x≥2
可得y=x-2代入①得
 ,解得x=2-y
,解得x=2-y又点B(x,y)是半圆x2+y2=1(y>0)上的一个动点
所以有(x-2)2+(y-2)2=1(x≥2)
故点C的轨迹方程是(x-2)2+(y-2)2=1(x≥2)
点评:本题考查求轨迹方程,解题的关键是理解题意,建立起已知轨迹方程的曲线上的点B的坐标与要求的轨迹方程的曲线上的点C的坐标之间的关系,再代入已知的轨迹方程,整理得出要求的轨迹方程,此过程称为代入法,其步骤为未知表示已知,再代入已知得出要求的轨迹方程,本题由垂直与线段相等两个关系建立方程,由于都是符号运算,运算量较大,变形时要严谨,不要因为运算出错,导致解题失败,由解题过程可以看出,此类题求解规律固定,入手一般是从找等量关系开始,切记!

练习册系列答案
相关题目
 已知半椭圆
已知半椭圆 和半圆x2+y2=b2(y≤0)组成曲线C,其中a>b>0;如图,半椭圆
和半圆x2+y2=b2(y≤0)组成曲线C,其中a>b>0;如图,半椭圆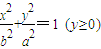 内切于矩形ABCD,且CD交y轴于点G,点P是半圆x2+y2=b2(y≤0)上异于A,B的任意一点,当点P位于点
内切于矩形ABCD,且CD交y轴于点G,点P是半圆x2+y2=b2(y≤0)上异于A,B的任意一点,当点P位于点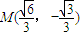 时,△AGP的面积最大.
时,△AGP的面积最大.