题目内容
(本小题满分12分)
已知函数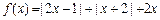 (
(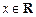 ),
),
(Ⅰ)求函数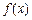 的最小值;
的最小值;
(Ⅱ)已知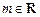 ,命题p:关于x的不等式
,命题p:关于x的不等式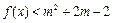 解集是空集;命题q:关于x的方程
解集是空集;命题q:关于x的方程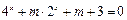 有实数根.若“p或q”为真,“p且q”为假,求实数m的取值
有实数根.若“p或q”为真,“p且q”为假,求实数m的取值 范围.
范围.
已知函数
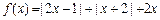 (
(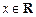 ),
),(Ⅰ)求函数
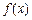 的最小值;
的最小值;(Ⅱ)已知
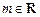 ,命题p:关于x的不等式
,命题p:关于x的不等式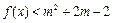 解集是空集;命题q:关于x的方程
解集是空集;命题q:关于x的方程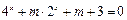 有实数根.若“p或q”为真,“p且q”为假,求实数m的取值
有实数根.若“p或q”为真,“p且q”为假,求实数m的取值 范围.
范围.(1)1
(2)
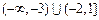
解:(Ⅰ)由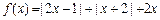 得
得
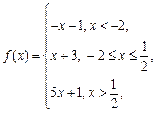 作出函数
作出函数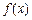 的图象,
的图象,
可知函数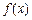 在
在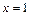 处取得最小值1. 4分
处取得最小值1. 4分
(Ⅱ)不等式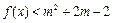 解集是空集,故
解集是空集,故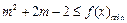 ,
,
由(Ⅰ)得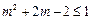
 ,即
,即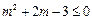 ,解得
,解得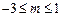 ,
,
∴命 题p:
题p: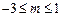 . 6分
. 6分
对于命题q,由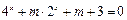 得
得
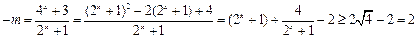 ,当且仅当
,当且仅当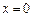 时“=”成立.解得
时“=”成立.解得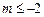 ,即命题q:
,即命题q: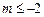 . 8分
. 8分
由“p或q”为真,“p且q”为假可知有以下两个情形:
若p真q假,则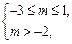 解得
解得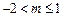 ; 10分
; 10分
若p假q真,则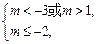 解得
解得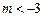 .
.
故实数m的取值范围是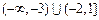 . 12分
. 12分
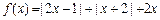 得
得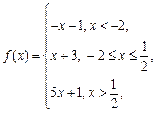 作出函数
作出函数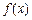 的图象,
的图象,可知函数
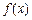 在
在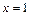 处取得最小值1. 4分
处取得最小值1. 4分(Ⅱ)不等式
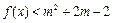 解集是空集,故
解集是空集,故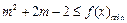 ,
,由(Ⅰ)得
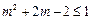
 ,即
,即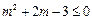 ,解得
,解得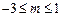 ,
,∴命
 题p:
题p: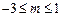 . 6分
. 6分对于命题q,由
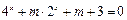 得
得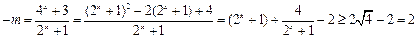 ,当且仅当
,当且仅当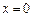 时“=”成立.解得
时“=”成立.解得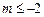 ,即命题q:
,即命题q: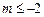 . 8分
. 8分由“p或q”为真,“p且q”为假可知有以下两个情形:
若p真q假,则
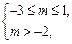 解得
解得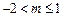 ; 10分
; 10分若p假q真,则
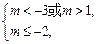 解得
解得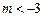 .
.故实数m的取值范围是
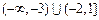 . 12分
. 12分
练习册系列答案
相关题目
 满足:“对于区间(1,2)上的任意实数
满足:“对于区间(1,2)上的任意实数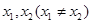 ,
,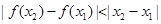 恒成立”,则称
恒成立”,则称



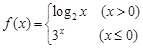 ,则
,则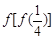 的值是( ).
的值是( ).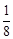 C. 9 D.
C. 9 D. 
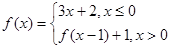 ,则
,则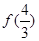 的值为( )
的值为( )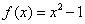 ,对任意
,对任意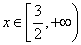 ,
,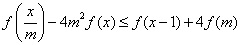 恒成立,求:实数
恒成立,求:实数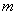 的取值范围。
的取值范围。 ,则
,则 ( )
( )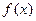 是定义在R上的增函数,且
是定义在R上的增函数,且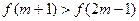 ,
,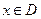 ,均有
,均有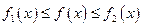 成立,则称函数
成立,则称函数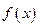 为函数
为函数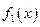 到函数
到函数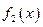 在区间
在区间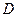 上的“折中函数”.已知函数
上的“折中函数”.已知函数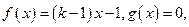
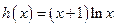 ,且
,且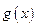 到
到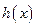 在区间
在区间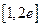 上的“折中函数”,则实数
上的“折中函数”,则实数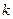 的取值范围为 ▲ .
的取值范围为 ▲ . 满足
满足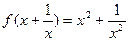 ,则
,则