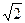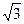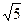题目内容
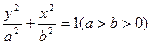
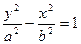 上在第一象限内的一点,直线PA、PB分别交椭圆于C、D点,如果D恰
上在第一象限内的一点,直线PA、PB分别交椭圆于C、D点,如果D恰是PB 的中点.
(1)求证:无论常数a、b如何,直线CD的斜率恒为定值;
(2)求双曲线的离心率,使CD通过椭圆的上焦点.
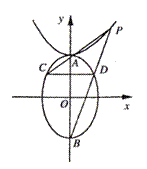
(2)
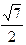
(1)设P点坐标为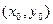 ,又A、B坐标分别是
,又A、B坐标分别是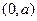 、
、
而D是PB的中点,∴D点坐标为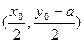 ,……………………2分
,……………………2分
把D点坐标代入椭圆方程,得: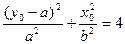 ①
①
又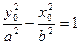 ②
②
由①②解得,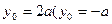 舍去)
舍去)
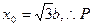 点坐标为
点坐标为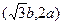 ………………………………5分
………………………………5分
故 ,直线PA的方程是
,直线PA的方程是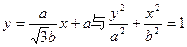 联立,解得
联立,解得
C点坐标为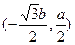 ,又D点坐标为
,又D点坐标为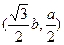 ……………………7分
……………………7分
∴C、D两点关于y轴对称,故无论a、b如何变化,都有CD//x轴,直线CD的斜率恒
为常常0.……………………9分
(2)当CD过椭圆焦点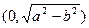 时,则
时,则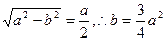 ,……10分
,……10分
双曲线中,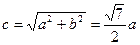 ,
,
∴双曲线的离心率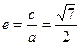 .………………………………12分
.………………………………12分
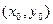 ,又A、B坐标分别是
,又A、B坐标分别是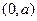 、
、
而D是PB的中点,∴D点坐标为
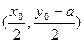 ,……………………2分
,……………………2分把D点坐标代入椭圆方程,得:
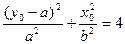 ①
①又
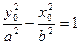 ②
②由①②解得,
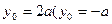 舍去)
舍去)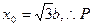 点坐标为
点坐标为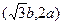 ………………………………5分
………………………………5分故
 ,直线PA的方程是
,直线PA的方程是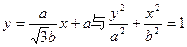 联立,解得
联立,解得C点坐标为
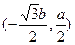 ,又D点坐标为
,又D点坐标为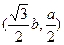 ……………………7分
……………………7分∴C、D两点关于y轴对称,故无论a、b如何变化,都有CD//x轴,直线CD的斜率恒
为常常0.……………………9分
(2)当CD过椭圆焦点
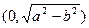 时,则
时,则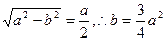 ,……10分
,……10分双曲线中,
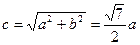 ,
,∴双曲线的离心率
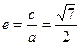 .………………………………12分
.………………………………12分
练习册系列答案
相关题目
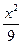 -
-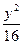 =1的两个焦点,P在双曲线上且满足|PF1|·|PF2|=32,则∠F1PF2=__________.
=1的两个焦点,P在双曲线上且满足|PF1|·|PF2|=32,则∠F1PF2=__________.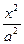 -
- =1(a>0,b>0)的左焦点且垂直于x轴的直线与双曲线交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于___________.
=1(a>0,b>0)的左焦点且垂直于x轴的直线与双曲线交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率等于___________.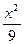 -
-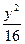 =1只有一个公共点的直线共有______________条.
=1只有一个公共点的直线共有______________条.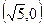 和曲线
和曲线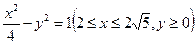 上的点
上的点 …、
…、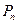 。若
。若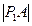 、
、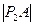 、…、
、…、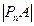 成等差数列且公差d >0,(1). 试将d表示为n的函数关系式.(2). 若
成等差数列且公差d >0,(1). 试将d表示为n的函数关系式.(2). 若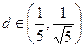 ,是否存在满足条件的
,是否存在满足条件的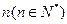 .若存在,求出n可取的所有值,若不存在,说明理由.
.若存在,求出n可取的所有值,若不存在,说明理由.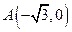 和
和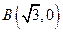 ,动点C到A、B两点的距离之差的绝对值为2,点C的轨迹与直线
,动点C到A、B两点的距离之差的绝对值为2,点C的轨迹与直线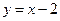 交于D、E两点,求线段DE的长.
交于D、E两点,求线段DE的长.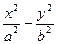 =1的右焦点,斜率k=2,若l与双曲线的两个交点分别在双曲线左、右两支上,则双曲线的离心率e的取值范围是( )
=1的右焦点,斜率k=2,若l与双曲线的两个交点分别在双曲线左、右两支上,则双曲线的离心率e的取值范围是( )