题目内容
11.已知直线2x-y+4=0与圆C1:x2+y2+2x-4y+F=0相交于A、B两点,若以弦AB为直径的圆C2经过点P(1,2),则F=( )| A. | -5 | B. | -1 | C. | 1 | D. | 5 |
分析 圆C1:x2+y2+2x-4y+F=0的圆心为(-1,2)在直线2x-y+4=0上,利用以弦AB为直径的圆C2经过点P(1,2),可得12+22+2-8+F=0,即可求出F.
解答 解:圆C1:x2+y2+2x-4y+F=0的圆心为(-1,2)在直线2x-y+4=0上,
因为以弦AB为直径的圆C2经过点P(1,2),
所以12+22+2-8+F=0,
所以F=1,
故选:C.
点评 本题主要考查直线和圆相交的性质,考查学生的计算能力,属于基础题.

练习册系列答案
 单元期中期末卷系列答案
单元期中期末卷系列答案
相关题目
20.将函数y=sin(2x+θ)的图象向右平移$\frac{π}{6}$个单位,得到的图象关于x=$\frac{π}{4}$对称,则θ的一个可能的值为( )
| A. | -$\frac{2}{3}π$ | B. | $\frac{2}{3}π$ | C. | -$\frac{5}{6}π$ | D. | $\frac{5}{6}π$ |

 为正实数,则当
为正实数,则当 的最小值为
的最小值为 时,不等式
时,不等式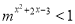 解集为_________.
解集为_________.