题目内容
19.在直角坐标系xOy中,两坐标系取相同的长度单位,将曲线$\left\{\begin{array}{l}x=5cosθ\\ y=sinθ\end{array}$(θ为参数)上每一点的横坐标变为原来的$\frac{1}{5}$(纵坐标不变),然后将所得图象向右平移2个单位,再向上平移3个单位得到曲线C;以原点O为极点,x轴的非负半轴为极轴建立极坐标系,已知直线l的极坐标方程为$ρsin(α-\frac{π}{4})=\sqrt{2}$.(Ⅰ)求曲线C的普通方程;
(Ⅱ)设直线l与曲线C交于A、B两点,与x轴交于点P,求|PA|•|PB|的值.
分析 (I)利用曲线横坐标的变换,将所得图象向右平移2个单位,再向上平移3个单位得到曲线$\left\{\begin{array}{l}x=cosθ+2\\ y=sinθ+3\end{array}\right.$,消去θ得曲线C的普通方程.
(II)设直线l直角坐标方程是y=x+2,求出直线l参数方程,代入曲线C求出t1t2=24.得到结果.
解答 解:(I)曲线$\left\{\begin{array}{l}x=5cosθ\\ y=sinθ\end{array}\right.$上每一点的横坐标变为原来的$\frac{1}{5}$,得到$\left\{\begin{array}{l}x=cosθ\\ y=sinθ\end{array}\right.$,
将所得图象向右平移2个单位,再向上平移3个单位得到曲线$\left\{\begin{array}{l}x=cosθ+2\\ y=sinθ+3\end{array}\right.$,
消去θ得曲线C的普通方程是(x-2)2+(y-3)2=1;…(5分)
(II)设直线l直角坐标方程是y=x+2,∴P(-2,0),
直线l倾斜角是45°,参数方程是$\left\{\begin{array}{l}x=-2+\frac{{\sqrt{2}}}{2}t\\ y=\frac{{\sqrt{2}}}{2}t\end{array}\right.$(t为参数),
代入曲线C得${t^2}-7\sqrt{2}t+24=0$,
△=2>0,t1t2=24,
∴|PA|•|PB|=|t1t2|=24.…(10分)
点评 本题考查曲线的参数方程以及极坐标方程的应用,考查计算能力.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
12.设等差数列{an}的前n项和为Sn,且满足S19>0,S20<0,则$\frac{{S}_{1}}{{a}_{1}}$,$\frac{{S}_{2}}{{a}_{2}}$,$\frac{{S}_{3}}{{a}_{3}}$,…,$\frac{{S}_{19}}{{a}_{19}}$中最大项为( )
| A. | $\frac{{S}_{8}}{{a}_{8}}$ | B. | $\frac{{S}_{9}}{{a}_{9}}$ | C. | $\frac{{S}_{10}}{{a}_{10}}$ | D. | $\frac{{S}_{11}}{{a}_{11}}$ |
8.设tanα、tanβ是方程x2-3x+2=0的两个根,则tan(α+β)=( )
| A. | -3 | B. | 3 | C. | -1 | D. | 1 |
4. 设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是( )
设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是( )
 设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是( )
设(x1,y1),(x2,y2),…,(xn,yn)是变量x和y的n个样本点,直线l是由这些样本点通过最小二乘法得到的线性回归方程(如图),以下结论中正确的是( )| A. | x和y正相关 | |
| B. | x和y的相关系数在-1到0之间 | |
| C. | x和y的相关系数为直线l的斜率 | |
| D. | 当n为偶数时,分布在l两侧的样本点的个数一定相同 |
 已知△ABC中,AB=AC,D为△ABC外接圆劣弧$\widehat{AC}$上的点(不与点A,C重合),延长BD至E,延长AD交BC的延长线于F
已知△ABC中,AB=AC,D为△ABC外接圆劣弧$\widehat{AC}$上的点(不与点A,C重合),延长BD至E,延长AD交BC的延长线于F 服从正态分布
服从正态分布 ,则
,则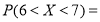 ( )
( )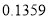 B.
B.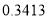 C.
C. D.1
D.1