题目内容
3.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的一个焦点是抛物线y2=8x的焦点,且双曲线 C的离心率为2,那么双曲线C的方程为x2-$\frac{{y}^{2}}{3}$=1;渐近线方程是y=±$\sqrt{3}x$.分析 根据抛物线的焦点(2,0)便得到c=2,而根据双曲线C的离心率即可得到$\frac{2}{a}=2$,所以a=1,所以得出b2=3,这样即可得出双曲线C的方程以及渐近线方程.
解答 解:抛物线的焦点为(2,0);
∴c=2;
∴根据双曲线的离心率为2得:$\frac{2}{a}=2$;
∴a=1,b2=3;
∴双曲线C的方程为${x}^{2}-\frac{{y}^{2}}{3}=1$;
∴其渐近线方程为y=$±\sqrt{3}x$.
故答案为:${x}^{2}-\frac{{y}^{2}}{3}=1$,$y=±\sqrt{3}x$.
点评 考查抛物线的焦点的概念及求法,双曲线焦点的概念,双曲线离心率的计算公式,以及由双曲线方程求渐近线方程的方法.

练习册系列答案
相关题目
16.已知集合A={x|-1≤x≤1},B={x|0≤x≤2},则A∩B=( )
| A. | [-1,0) | B. | [-1,0] | C. | [0,1] | D. | (-∞,1)∪[2,+∞) |
 已知△ABC中,AB=AC,D为△ABC外接圆劣弧$\widehat{AC}$上的点(不与点A,C重合),延长BD至E,延长AD交BC的延长线于F
已知△ABC中,AB=AC,D为△ABC外接圆劣弧$\widehat{AC}$上的点(不与点A,C重合),延长BD至E,延长AD交BC的延长线于F .
. 时,求函数
时,求函数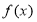 的最大值;
的最大值;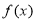 与
与 轴交于两点
轴交于两点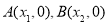 且
且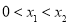 ,证明:
,证明: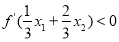 .
. ,
,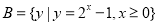 ,则
,则 ( )
( ) B.
B.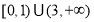 C.
C. D.
D.