题目内容
3.若某几何体的三视图如图所示,则这个几何体中最长的棱长等于$\sqrt{33}$,体积等于$\frac{16}{3}$.
分析 可以得出空间几何体是如下图:三棱锥,运用空间几何体的性质,求解边长,面积体积,计算准确,可以得出答案.
解答 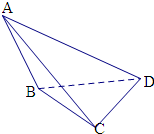 解:可以得出空间几何体是如右图:
解:可以得出空间几何体是如右图:
BD=4,BC=CD=2$\sqrt{2}$,
运用三视图得出:AC=$\sqrt{16+1}$=$\sqrt{17}$,AB=$\sqrt{5}$,
根据这个几何体得出:PB=$\sqrt{16+5}$=$\sqrt{21}$,PC=$\sqrt{16+17}$=$\sqrt{33}$,PD=$\sqrt{16+1}$=$\sqrt{17}$,
∴这个几何体中最长的棱长等于$\sqrt{33}$,
底面积为:$\frac{1}{2}×$4×2=4
体积为:$\frac{1}{3}×$($\frac{1}{2}×$4×2)×4=$\frac{16}{3}$
故答案为:$\sqrt{33}$,$\frac{16}{3}$.
点评 本题考查了运用几何体的三视图求解棱长,体积,属于计算题,关键是运用三视图恢复空间几何体的原图.

练习册系列答案
相关题目
16.已知集合A={x|-1≤x≤1},B={x|0≤x≤2},则A∩B=( )
| A. | [-1,0) | B. | [-1,0] | C. | [0,1] | D. | (-∞,1)∪[2,+∞) |
12.设等差数列{an}的前n项和为Sn,且满足S19>0,S20<0,则$\frac{{S}_{1}}{{a}_{1}}$,$\frac{{S}_{2}}{{a}_{2}}$,$\frac{{S}_{3}}{{a}_{3}}$,…,$\frac{{S}_{19}}{{a}_{19}}$中最大项为( )
| A. | $\frac{{S}_{8}}{{a}_{8}}$ | B. | $\frac{{S}_{9}}{{a}_{9}}$ | C. | $\frac{{S}_{10}}{{a}_{10}}$ | D. | $\frac{{S}_{11}}{{a}_{11}}$ |
19.已知双曲线C:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的渐近线方程为y=±$\frac{1}{2}$x,则其离心率为( )
| A. | $\frac{\sqrt{5}}{2}$ | B. | $\sqrt{5}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\sqrt{3}$ |
8.设tanα、tanβ是方程x2-3x+2=0的两个根,则tan(α+β)=( )
| A. | -3 | B. | 3 | C. | -1 | D. | 1 |
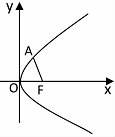 已知抛物线y2=2px的焦点为F,若该抛物线上有一点A,满足直线FA的倾斜角为120°,且|FA|=4,
已知抛物线y2=2px的焦点为F,若该抛物线上有一点A,满足直线FA的倾斜角为120°,且|FA|=4,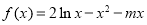 .
. 时,求函数
时,求函数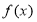 的最大值;
的最大值;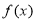 与
与 轴交于两点
轴交于两点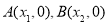 且
且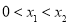 ,证明:
,证明: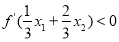 .
.