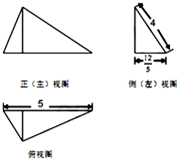
题目内容
5.数列{an}中,a1=60,且an+1=an-3,求这个数列前n项和Sn的最大值.分析 通过等差数列的求和公式、配方可知Sn=-$\frac{3}{2}$•$(n-\frac{41}{2})^{2}$+$\frac{5043}{8}$,进而计算可得结论.
解答 解:依题意,数列{an}是以60为首项、-3为公差的等差数列,
∴Sn=60n-3$•\frac{n(n-1)}{2}$
=-$\frac{3}{2}$•$(n-\frac{41}{2})^{2}$+$\frac{5043}{8}$,
又∵S20=S21=-$\frac{3}{2}$•$\frac{1}{4}$+$\frac{5043}{8}$=630,
∴Sn的最大值为630.
点评 本题考查数列的求和,注意解题方法的积累,属于基础题.

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目