题目内容
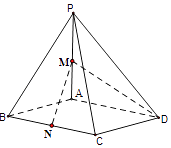
【题目】如图平行四边形ABCD中,∠DAB=60°,AB=2,AD=2,M为CD边的中点,沿BM将△CBM折起使得平面BMC⊥平面ABMD. 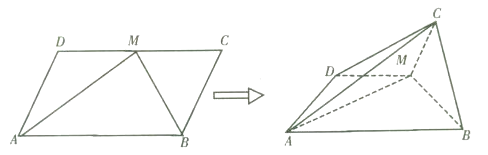
(1)求四棱锥C﹣ADMB的体积;
(2)求折后直线AB与平面AMC所成的角的正弦.
【答案】
(1)解:由已知∠DAB=60°,AB=AD=2,
M为边CD的中点,
∴△CMB是等边三角形,
取MB的中点O,则CO⊥MB,
又平面BMC⊥平面ABMD于MB,
则CO⊥平面ABMD,且CO= ![]() .
.
![]() =
= ![]() =
= ![]() ,
,
∴V四棱锥C﹣ADMB= ![]()
(2)解:∵∠DAB=60°,AB=AD=2,
M为边CD的中点,
∴AM=2 ![]() ,BM=2,
,BM=2,
∴AM⊥BM,
又平面BMC⊥平面ABMD交线为BM,
∴AM⊥平面CMB,
∴平面AMC⊥平面BMC于MC,
由△CMB是等边三角形,取CM的中点E,连接BE,则BE⊥CM,
∴BE⊥平面AMC,连接EA,则∠BAE是直线AB与平面AMC所成的角,
∴sin∠BAE= ![]() =
= ![]() =
= ![]() .
.
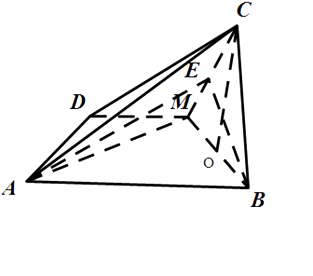
【解析】(1)由已知得△CMB是等边三角形,取MB的中点O,则CO⊥MB,又平面BMC⊥平面ABMD,CO= ![]() ,求出底面梯形的面积,再利用棱锥的体积公式解答;(2)利用面面垂直的性质和判定,找到折后直线AB与面AMC所成的角的平面角,然后求正弦值即可.
,求出底面梯形的面积,再利用棱锥的体积公式解答;(2)利用面面垂直的性质和判定,找到折后直线AB与面AMC所成的角的平面角,然后求正弦值即可.
【考点精析】解答此题的关键在于理解空间角的异面直线所成的角的相关知识,掌握已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则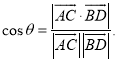 .
.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目