题目内容
(本小题满分12分)已知在直角坐标系xoy中,曲线 的参数方程为
的参数方程为
(t为非零常数, 为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以
为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线 的方程为
的方程为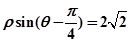 .
.
(Ⅰ)求曲线C的普通方程并说明曲线的形状;
(Ⅱ)是否存在实数 ,使得直线
,使得直线 与曲线C有两个不同的公共点
与曲线C有两个不同的公共点 、
、 ,且
,且
(其中o为坐标原点)?若存在,请求出;否则,请说明理由
 的参数方程为
的参数方程为
(t为非零常数,
 为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以
为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线 的方程为
的方程为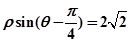 .
.(Ⅰ)求曲线C的普通方程并说明曲线的形状;
(Ⅱ)是否存在实数
 ,使得直线
,使得直线 与曲线C有两个不同的公共点
与曲线C有两个不同的公共点 、
、 ,且
,且
(其中o为坐标原点)?若存在,请求出;否则,请说明理由
(Ⅰ)∵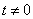 ,∴可将曲线C的方程化为普通方程:
,∴可将曲线C的方程化为普通方程: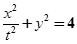 .
.
①当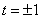 时,曲线C为圆心在原点,半径为2的圆;
时,曲线C为圆心在原点,半径为2的圆;
②当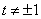 时,曲线C为中心在原点的椭圆.
时,曲线C为中心在原点的椭圆.
(Ⅱ)不存在满足题意的实数 .
.
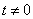 ,∴可将曲线C的方程化为普通方程:
,∴可将曲线C的方程化为普通方程: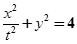 .
. ①当
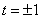 时,曲线C为圆心在原点,半径为2的圆;
时,曲线C为圆心在原点,半径为2的圆; ②当
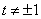 时,曲线C为中心在原点的椭圆.
时,曲线C为中心在原点的椭圆. (Ⅱ)不存在满足题意的实数
 .
. (I)先把方程化成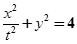 ,然后再根据t2与1的关系进行讨论.
,然后再根据t2与1的关系进行讨论.
(II)先求出直线l的普通方程为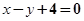 ,然后再与曲线C的方程联立消y得关于x的一元二次方程,由于
,然后再与曲线C的方程联立消y得关于x的一元二次方程,由于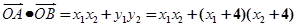 ,所以再借助韦达定理及判断式来解此题.
,所以再借助韦达定理及判断式来解此题.
解:(Ⅰ)∵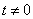 ,∴可将曲线C的方程化为普通方程:
,∴可将曲线C的方程化为普通方程: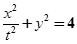 .
.
①当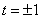 时,曲线C为圆心在原点,半径为2的圆;
时,曲线C为圆心在原点,半径为2的圆;
②当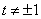 时,曲线C为中心在原点的椭圆.………………5分
时,曲线C为中心在原点的椭圆.………………5分
(Ⅱ)直线 的普通方程为:
的普通方程为: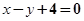 .联立直线与曲线的方程,消
.联立直线与曲线的方程,消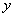 得
得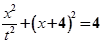 ,
,
化简得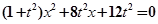 .若直线
.若直线 与曲线C有两个不同的公共点,
与曲线C有两个不同的公共点,
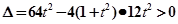 ,
,
解得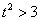 .又
.又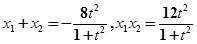
故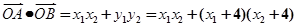
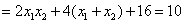 .
.
解得 与
与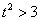 相矛盾. 故不存在满足题意的实数
相矛盾. 故不存在满足题意的实数 . ………………12分
. ………………12分
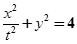 ,然后再根据t2与1的关系进行讨论.
,然后再根据t2与1的关系进行讨论.(II)先求出直线l的普通方程为
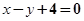 ,然后再与曲线C的方程联立消y得关于x的一元二次方程,由于
,然后再与曲线C的方程联立消y得关于x的一元二次方程,由于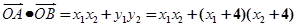 ,所以再借助韦达定理及判断式来解此题.
,所以再借助韦达定理及判断式来解此题.解:(Ⅰ)∵
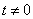 ,∴可将曲线C的方程化为普通方程:
,∴可将曲线C的方程化为普通方程: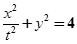 .
. ①当
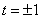 时,曲线C为圆心在原点,半径为2的圆;
时,曲线C为圆心在原点,半径为2的圆; ②当
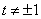 时,曲线C为中心在原点的椭圆.………………5分
时,曲线C为中心在原点的椭圆.………………5分(Ⅱ)直线
 的普通方程为:
的普通方程为: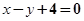 .联立直线与曲线的方程,消
.联立直线与曲线的方程,消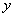 得
得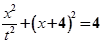 ,
,化简得
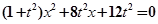 .若直线
.若直线 与曲线C有两个不同的公共点,
与曲线C有两个不同的公共点,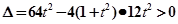 ,
,解得
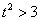 .又
.又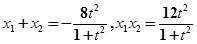
故
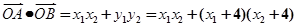
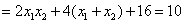 .
.解得
 与
与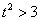 相矛盾. 故不存在满足题意的实数
相矛盾. 故不存在满足题意的实数 . ………………12分
. ………………12分
练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
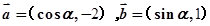 ,且
,且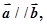
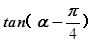 等于( )
等于( )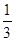
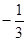
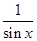 ,
,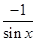 ),b=(2,cos2x).
),b=(2,cos2x). ],试判断a与b能否平行?
],试判断a与b能否平行?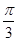 ],求函数f(x)=a·b的最小值.
],求函数f(x)=a·b的最小值. 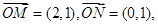 O为坐标原点,动点
O为坐标原点,动点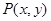 满足
满足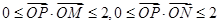 ,则
,则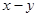 的最小值是
的最小值是 ,且
,且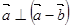 。
。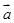 与
与 的夹角;
的夹角;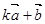 与
与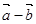 平行时,求实数
平行时,求实数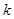 的值。
的值。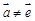 ,
,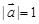 ,对任意
,对任意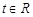 ,恒有
,恒有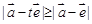 ,则
,则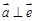
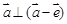
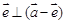
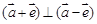
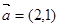 ,
, ,且
,且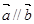 ,则
,则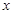 的值为( )
的值为( )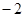
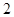
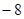
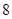
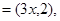 b=(6,1),若a∥b,则
b=(6,1),若a∥b,则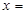 ( )
( )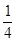

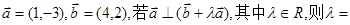 ___________.
___________.