题目内容
已知向量a=(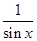 ,
,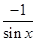 ),b=(2,cos2x).
),b=(2,cos2x).
(1)若x∈(0, ],试判断a与b能否平行?
],试判断a与b能否平行?
(2)若x∈(0,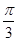 ],求函数f(x)=a·b的最小值.
],求函数f(x)=a·b的最小值.
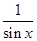 ,
,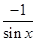 ),b=(2,cos2x).
),b=(2,cos2x).(1)若x∈(0,
 ],试判断a与b能否平行?
],试判断a与b能否平行?(2)若x∈(0,
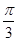 ],求函数f(x)=a·b的最小值.
],求函数f(x)=a·b的最小值. (1) a与b不能平行 (2) 2

本试题主要是考查而来向量的共线概念以及数量积的运算和三角函数性质的综合运用。
(1)因为若a与b平行,则有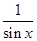 ·cos2x=
·cos2x=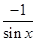 ·2,那么解方程可知方程无解。故a与b不能平行.
·2,那么解方程可知方程无解。故a与b不能平行.
(2)由于f(x)=a·b= -
- =
= =
= =2sinx+
=2sinx+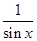 ,然后借助于均值不等式得到最值。
,然后借助于均值不等式得到最值。
解: (1)若a与b平行,则有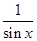 ·cos2x=
·cos2x=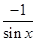 ·2, ……3分
·2, ……3分
因为x∈(0, ],sinx≠0,所以得cos2x=-2,这与|cos2x|≤1相矛盾,
],sinx≠0,所以得cos2x=-2,这与|cos2x|≤1相矛盾,
故a与b不能平行. ……7分
(2)由于f(x)=a·b= -
- =
= =
= =2sinx+
=2sinx+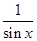 10分
10分
又因为x∈(0,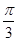 ],所以sinx∈(0,
],所以sinx∈(0, ],于是2sinx+
],于是2sinx+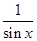 ≥2
≥2
=2 ,当2sinx=
,当2sinx=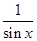 ,即sinx=
,即sinx= 时取等号.
时取等号.
故函数f(x)的最小值等于2 . ……14分
. ……14分
(1)因为若a与b平行,则有
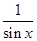 ·cos2x=
·cos2x=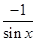 ·2,那么解方程可知方程无解。故a与b不能平行.
·2,那么解方程可知方程无解。故a与b不能平行.(2)由于f(x)=a·b=
 -
- =
= =
= =2sinx+
=2sinx+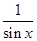 ,然后借助于均值不等式得到最值。
,然后借助于均值不等式得到最值。解: (1)若a与b平行,则有
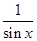 ·cos2x=
·cos2x=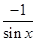 ·2, ……3分
·2, ……3分因为x∈(0,
 ],sinx≠0,所以得cos2x=-2,这与|cos2x|≤1相矛盾,
],sinx≠0,所以得cos2x=-2,这与|cos2x|≤1相矛盾,故a与b不能平行. ……7分
(2)由于f(x)=a·b=
 -
- =
= =
= =2sinx+
=2sinx+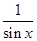 10分
10分又因为x∈(0,
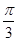 ],所以sinx∈(0,
],所以sinx∈(0, ],于是2sinx+
],于是2sinx+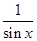 ≥2
≥2
=2
 ,当2sinx=
,当2sinx=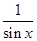 ,即sinx=
,即sinx= 时取等号.
时取等号.故函数f(x)的最小值等于2
 . ……14分
. ……14分
练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目
 且点P在线段
且点P在线段 的延长线上,且
的延长线上,且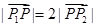 ,则点P的坐标为( )
,则点P的坐标为( ) 



 的参数方程为
的参数方程为
 为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以
为参数),在极坐标系(与直角坐标系xoy取相同的长度单位,且以原点O为极点,以 轴正半轴为极轴)中,直线
轴正半轴为极轴)中,直线 的方程为
的方程为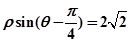 .
. ,使得直线
,使得直线 、
、 ,且
,且
 ),b=(-2,-2
),b=(-2,-2 ,
, ,若
,若 ⊥
⊥ ,则
,则 =_________
=_________ ,若
,若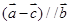 ,则k=________.
,则k=________.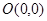
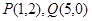 ,
, 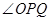 的平分线交
的平分线交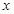 轴于点
轴于点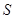 .记
.记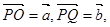 则
则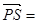 ( )
( )



 ,
,  满足条件
满足条件 ,则
,则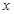 =__________
=__________  ,
, ,点
,点 是线段
是线段 上的点,且
上的点,且
 ,则
,则


