题目内容
已知函数f(x)的图象与函数y=ax-1,(a>1)的图象关于直线y=x对称,g(x)=loga(x2-3x+3)(a>1).(1)求函数f(x)的解析式;
(2)若函数f(x)在区间[m,n](m>-1)上的值域为
 ,求实数p的取值范围;
,求实数p的取值范围;(3)设函数F(x)=af(x)-g(x)(a>1),若w≥F(x)对一切x∈(-1,+∞)恒成立,求实数w的取值范围.
【答案】分析:(1)根据函数f(x)的图象与函数 y=ax的图象关于直线y=x对称可知两函数互为反函数,从而求出函数f(x)的解析式;
(2)根据函数的单调性建立等式关系,x2-3x+3=p+3x在( ,+∞)有两个不等的根,从而求出p的范围;
,+∞)有两个不等的根,从而求出p的范围;
另解:可转化为函数y=x2+x,x∈(-1,0)∪(0,+∞)图象与函数y=p的图象有两个交点问题,数形结合求解
(3)先求出函数F(x)的最大值,若w≥F(x)对一切x∈(-1,+∞)恒成立,转化为w≥F(x)max
解答:(本题满分18分)
解:(文科)(1)由已知得 f(x)=loga(x+1); (4分)
(2)∵a>1,∴f(x)在(-1,+∞)上为单调递增函数,(6分)∴在区间[m,n](m>-1), ,
, ;
;
即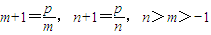 .∴m,n是方程
.∴m,n是方程
即方程x2+x-p=0,x∈(-1,0)∪(0,+∞)的两个相异的解,(8分)
这等价于 ,(10分) 解得
,(10分) 解得 为所求.(12分)
为所求.(12分)
另解:可转化为函数y=x2+x,x∈(-1,0)∪(0,+∞)图象与函数y=p的图象有两个交点问题,数形结合求得: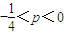 .
.
(3) (14分)∵
(14分)∵ ,当且仅当
,当且仅当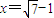 时等号成立,∴
时等号成立,∴ ,(16分)∴
,(16分)∴ ,∵w≥F(x)恒成立,∴w≥F(x)max,所以
,∵w≥F(x)恒成立,∴w≥F(x)max,所以 为所求.(18分)
为所求.(18分)
点评:题主要考查了函数解析式的求解,以及函数的值域和列举法,同时考查了分析问题,解决问题的能力,属于中档题.
(2)根据函数的单调性建立等式关系,x2-3x+3=p+3x在(
 ,+∞)有两个不等的根,从而求出p的范围;
,+∞)有两个不等的根,从而求出p的范围;另解:可转化为函数y=x2+x,x∈(-1,0)∪(0,+∞)图象与函数y=p的图象有两个交点问题,数形结合求解
(3)先求出函数F(x)的最大值,若w≥F(x)对一切x∈(-1,+∞)恒成立,转化为w≥F(x)max
解答:(本题满分18分)
解:(文科)(1)由已知得 f(x)=loga(x+1); (4分)
(2)∵a>1,∴f(x)在(-1,+∞)上为单调递增函数,(6分)∴在区间[m,n](m>-1),
 ,
, ;
;即
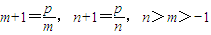 .∴m,n是方程
.∴m,n是方程
即方程x2+x-p=0,x∈(-1,0)∪(0,+∞)的两个相异的解,(8分)
这等价于
 ,(10分) 解得
,(10分) 解得 为所求.(12分)
为所求.(12分)另解:可转化为函数y=x2+x,x∈(-1,0)∪(0,+∞)图象与函数y=p的图象有两个交点问题,数形结合求得:
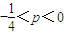 .
.(3)
 (14分)∵
(14分)∵ ,当且仅当
,当且仅当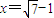 时等号成立,∴
时等号成立,∴ ,(16分)∴
,(16分)∴ ,∵w≥F(x)恒成立,∴w≥F(x)max,所以
,∵w≥F(x)恒成立,∴w≥F(x)max,所以 为所求.(18分)
为所求.(18分)点评:题主要考查了函数解析式的求解,以及函数的值域和列举法,同时考查了分析问题,解决问题的能力,属于中档题.

练习册系列答案
 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
已知函数f(x)的图象关于直线x=2对称,且当x≠2时其导函数f′(x)满足xf′(x)>2f′(x),若2<a<4,则下列表示大小关系的式子正确的是( )
| A、f(2a)<f(3)<f(log2a) | B、f(3)<f(log2a)<f(2a) | C、f(log2a)<f(3)<f(2a) | D、f(log2a)<f(2a)<f(3) |
 (2011•焦作一模)已知函数f(x)的图象过点(
(2011•焦作一模)已知函数f(x)的图象过点(