题目内容
已知向量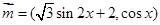 ,
,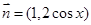 ,设函数
,设函数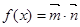 ,
,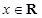 .
.
(Ⅰ)求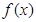 的最小正周期与最大值;
的最小正周期与最大值;
(Ⅱ)在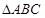 中,
中,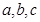 分别是角
分别是角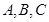 的对边,若
的对边,若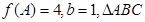 的面积为
的面积为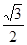 ,求
,求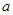 的值.
的值.
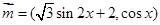 ,
,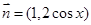 ,设函数
,设函数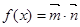 ,
,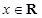 .
.(Ⅰ)求
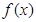 的最小正周期与最大值;
的最小正周期与最大值;(Ⅱ)在
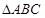 中,
中,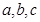 分别是角
分别是角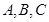 的对边,若
的对边,若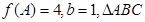 的面积为
的面积为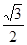 ,求
,求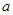 的值.
的值.(Ⅰ)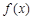 的最小正周期为
的最小正周期为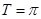 ,
,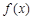 的最大值为5;(Ⅱ)
的最大值为5;(Ⅱ)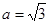 .
.
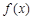 的最小正周期为
的最小正周期为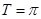 ,
,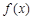 的最大值为5;(Ⅱ)
的最大值为5;(Ⅱ)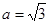 .
.试题分析:(Ⅰ)求
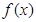 的最小正周期与最大值,首先须求出
的最小正周期与最大值,首先须求出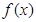 的解析式,由已知向量
的解析式,由已知向量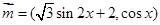 ,
,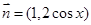 ,函数
,函数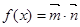 ,可将
,可将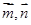 代入,根据数量积求得
代入,根据数量积求得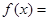
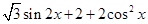 ,进行三角恒等变化,像这一类题,求周期与最大值问题,常常采用把它化成一个角的一个三角函数,即化成
,进行三角恒等变化,像这一类题,求周期与最大值问题,常常采用把它化成一个角的一个三角函数,即化成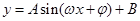 ,利用它的图象与性质,,求出周期与最大值,本题利用两角和与差的三角函数公式整理成
,利用它的图象与性质,,求出周期与最大值,本题利用两角和与差的三角函数公式整理成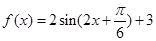 ,从而求得
,从而求得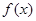 的最小正周期与最大值;(Ⅱ)在
的最小正周期与最大值;(Ⅱ)在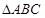 中,
中,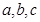 分别是角
分别是角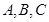 的对边,若
的对边,若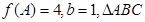 的面积为
的面积为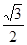 ,求
,求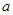 的值,要求
的值,要求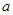 的值,一般用正弦定理或余弦定理,本题注意到
的值,一般用正弦定理或余弦定理,本题注意到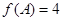 ,由
,由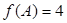 得,可求出角A的值,由已知
得,可求出角A的值,由已知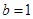 ,
,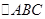 的面积为
的面积为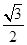 ,可利用面积公式
,可利用面积公式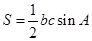 ,求出
,求出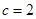 ,已知两边及夹角,可利用余弦定理求出
,已知两边及夹角,可利用余弦定理求出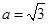 ,解此类题,主要分清边角关系即可,一般不难.
,解此类题,主要分清边角关系即可,一般不难.试题解析:(Ⅰ)
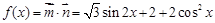
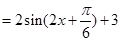 ,∴
,∴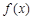 的最小正周期为
的最小正周期为 ,
,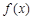 的最大值为5.
的最大值为5.(Ⅱ)由
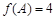 得,
得,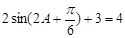 ,即
,即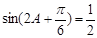 ,∵
,∵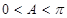 ,∴
,∴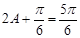 ,
,∴
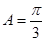 ,又
,又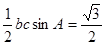 ,即
,即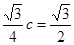 ,
,∴
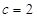 ,由余弦定理得,
,由余弦定理得,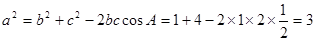
∴
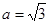

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
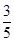 ,tan(α-β)=-
,tan(α-β)=-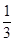 .求cosβ的值.
.求cosβ的值.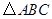 中,已知内角
中,已知内角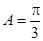 ,边
,边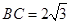 .设内角
.设内角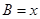 ,周长为
,周长为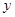 .
.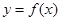 的解析式和定义域; (2)求
的解析式和定义域; (2)求 .
.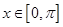 时,求
时,求 的最大值和最小值;
的最大值和最小值; 的内角
的内角 所对的边分别为
所对的边分别为 ,且
,且 ,若向量
,若向量 与向量
与向量 共线,求
共线,求 的值.
的值.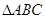 中,已知内角
中,已知内角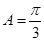 ,边
,边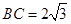 .设内角
.设内角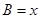 ,
,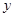 .
.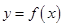 的解析式和定义域;
的解析式和定义域;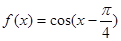 .
.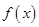 在区间
在区间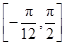 上的最大值和最小值;
上的最大值和最小值;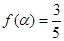 ,其中
,其中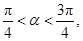 求
求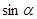 的值.
的值.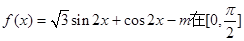 上有两个零点
上有两个零点 ,则
,则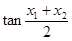 的值为( )
的值为( )



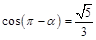 ,且
,且 ,则
,则 ( )
( )



 中,
中, ,
,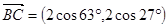 ,则
,则


