题目内容
【题目】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,求
,求![]() 的值;
的值;
(2)求函数![]() 的单调区间;
的单调区间;
(3)当![]() 时, 对
时, 对![]() ,使得
,使得![]() 成立, 则实数
成立, 则实数![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() ;(3)
;(3) ![]() .
.
【解析】
试题分析:(1)由导数的几何意义得 解得
解得![]() ;(2)求
;(2)求![]() ,由
,由![]() 得函数
得函数![]() 的单调区间;(3)求得
的单调区间;(3)求得![]() 在
在![]() 上的最大值
上的最大值![]() ,
,![]() 在
在![]() 上的最大值为
上的最大值为![]() 可得
可得![]() 的取值范围.
的取值范围.
试题解析:(1)![]() ,由于曲线
,由于曲线![]() 在点
在点![]() 处的切线方程为
处的切线方程为![]() ,所以
,所以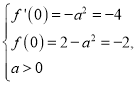 解得
解得![]() .
.
(2)令![]() ,即
,即![]() ,解得
,解得![]() ,由
,由![]() ,得
,得![]() ,或
,或![]() ,
,
由![]() ,得
,得![]() ,所以
,所以![]() 的单调增区间为
的单调增区间为![]() ,单调减区间为
,单调减区间为![]() .
.
(3)“对![]() , 使
, 使![]() 成立” 等价于“
成立” 等价于“![]() 在
在![]() 上的最大值
上的最大值
小于![]() 在
在![]() 上的最大值”.当
上的最大值”.当![]() 时,
时,![]() . 由(2)可得
. 由(2)可得![]() 与
与![]()
在![]() 上的情况如下:
上的情况如下:
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
|
|
|
|
|
|
由上表可知![]() 在
在![]() 上的最大值
上的最大值![]() .因为
.因为![]() 在
在![]() 上恒成立,所以
上恒成立,所以![]() 在
在![]() 上单调递增. 所以最大值为
上单调递增. 所以最大值为![]() .由
.由![]() ,即
,即![]() ,得
,得![]() ,故
,故![]() 的取值范围为
的取值范围为![]() .
.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目