题目内容
【题目】已知两点M（﹣3，0），N（3，0），点P为坐标平面内一动点，且
，则动点P（x，y）到两点A（﹣3，0）、B（﹣2，3）的距离之和的最小值为（ ）
A. 4 B. 5 C. 6 D. 
【答案】B
【解析】
首先利用向量数量积的运算求出抛物线的方程，然后根据抛物线的定义再将动点P（x，y）到点A（﹣3，0）的距离转化为到焦点的距离，进而转化为到准线的距离，如图．再由抛物线的性质知：当B，C和P三点共线的时候距离之和最小，从而得到答案．
设P（x，y），因为M（﹣3，0），N（3，0），
所以
，
，
=（6，0），
由
，则
，
化简整理得y2=﹣12x，其焦点坐标为（﹣3，0），
所以点A是抛物线y2=﹣12x的焦点，
过P作准线x=3的垂线，垂足为C，
则动点P（x，y）到两点A（﹣3，0）、B（﹣2，3）的距离之和等于动点P（x，y）到点B（﹣2，3）和到直线x=3的距离之和，
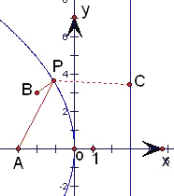
依题意可知当B，C和P三点共线的时候，距离之和最小，如图，
最小值为：3﹣（﹣2）=5．
故选：B．
练习册系列答案
口算题卡加应用题集训系列答案
综合自测系列答案
相关题目
