题目内容
P是抛物线x2=
(y-1)上的动点,点A(0,-1),点M在直线PA上且分PA所成的比为2:1,则点M的轨迹方程是( )
| 1 |
| 2 |
分析:设出M的坐标,利用点M分
所成的比为2,求出P的坐标,代入抛物线方程即可.
| PA |
解答:解:设M(x,y)、p(x′,y′),由题意可知
=2
,
即:
,所以
,
因为p(x′,y′)在抛物线上,所以(3y+2)-1=2(3x)2,
所以点M的轨迹方程为:y=6x2-
,即x2=
(y+
).
故选A.
| PM |
| MA |
即:
|
|
因为p(x′,y′)在抛物线上,所以(3y+2)-1=2(3x)2,
所以点M的轨迹方程为:y=6x2-
| 1 |
| 3 |
| 1 |
| 6 |
| 1 |
| 3 |
故选A.
点评:本题是基础题,考查圆锥曲线的轨迹方程的求法,注意相关点法的应用.

练习册系列答案
相关题目
 已知椭圆C的中心在原点,离心率等于
已知椭圆C的中心在原点,离心率等于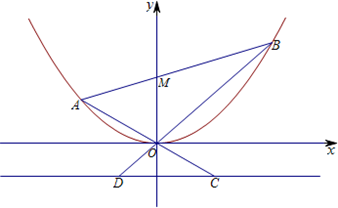 已知抛物线E:x2=4y,直线l过点M(0,2)且与抛物线交于A、B两点,直线OA、OB分别与抛物线的准线l0交于C、D.
已知抛物线E:x2=4y,直线l过点M(0,2)且与抛物线交于A、B两点,直线OA、OB分别与抛物线的准线l0交于C、D.