题目内容
已知抛物线x2=4y，点P是抛物线上的动点，点A的坐标为（12，6），求点P到点A的距离与到x轴的距离之和的最小值．
分析：如图所示，过P点作PB⊥l于点B，交x轴于点C，利用抛物线的定义可得PA+PC=PA+PB-1=PA+PF-1，可知当点A、P、F三点共线，因此PA+PF取得最小值FA，求出即可．
解答：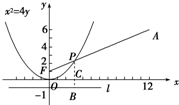
解：将x=12代入x2=4y，得y=36＞6，
所以点A在抛物线外部．抛物线焦点为F（0，1），准线l：y=-1．
如图所示，过P点作PB⊥l于点B，交x轴于点C，
则PA+PC=PA+PB-1=PA+PF-1．
由图可知，当A、P、F三点共线时，PA+PF的值最小，
所以PA+PF的最小值为FA=13，
故PA+PC的最小值为12．
解：将x=12代入x2=4y，得y=36＞6，所以点A在抛物线外部．抛物线焦点为F（0，1），准线l：y=-1．
如图所示，过P点作PB⊥l于点B，交x轴于点C，
则PA+PC=PA+PB-1=PA+PF-1．
由图可知，当A、P、F三点共线时，PA+PF的值最小，
所以PA+PF的最小值为FA=13，
故PA+PC的最小值为12．
点评：本题主要考查了抛物线的简单性质，熟练掌握抛物线的定义及其三点共线时PA+PF取得最小值是解题的关键．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知抛物线x2=4y上的点P（非原点）处的切线与x轴，y轴分别交于Q，R两点，F为焦点．
（2009•温州一模）如图，已知抛物线x2=4y，过抛物线上一点A（x1，y1）（不同于顶点）作抛物线的切线l，并交x轴于点C，在直线y=-1上任取一点H，过H作HD垂直x轴于D，并交l于点E，过H作直线HF垂直直线l，并交x轴于点F．
（2011•浙江模拟）已知抛物线x2=4y，圆C：x2+（y-2）2=4，M（x0，y0），（x0＞0，y0＞0）为抛物线上的动点．