题目内容
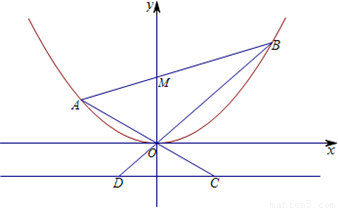
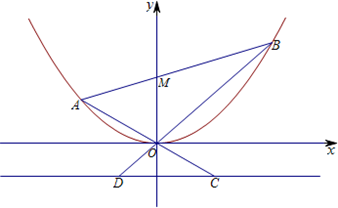 已知抛物线E:x2=4y,直线l过点M(0,2)且与抛物线交于A、B两点,直线OA、OB分别与抛物线的准线l0交于C、D.
已知抛物线E:x2=4y,直线l过点M(0,2)且与抛物线交于A、B两点,直线OA、OB分别与抛物线的准线l0交于C、D.(1)若点P是抛物线y=
| 1 |
| 6 |
| 1 |
| 2 |
(2)求证:
| OA |
| OB |
(3)求CD的最小值.
分析:(1)设P(x0,
x02+
),抛物线E:x2=4y的准线方程l0为y=-1.由点P在直线l0上的射影为Q,知PQ=
x02+
,由M(0,2),知PM=
=
x02+
,由此能够证明PQ=PM.
(2)由题设知直线AB的斜率一定存在,设AB:y=kx+2,由
,得x2-4kx-8=0,设A(x1,y1),B(x2,y2),则x1+x2=4k,x1•x2=-8,y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4=-8k2+8k2+4=4,由此能够证明
•
为定值.
(3)由A(x1,y1),B(x2,y2),O(0,0),C,D都在直线l0:y=-1上,知C(-
,-1),D(-
,-1),故CD=|
-
|=
=
=
,由此能求出CD的最小值.
| 1 |
| 6 |
| 1 |
| 2 |
| 1 |
| 6 |
| 3 |
| 2 |
(x0-0)2+(
|
| 1 |
| 6 |
| 3 |
| 2 |
(2)由题设知直线AB的斜率一定存在,设AB:y=kx+2,由
|
| OA |
| OB |
(3)由A(x1,y1),B(x2,y2),O(0,0),C,D都在直线l0:y=-1上,知C(-
| x2 |
| y2 |
| x1 |
| y1 |
| x2 |
| y2 |
| x1 |
| y1 |
| |x2y1-x1y2| |
| y1y2 |
| |x2(kx1+2)-x1(kx2+2)| |
| 4 |
| |x1-x2| |
| 2 |
解答:解:(1)∵点P是抛物线y=
x2+
上任意一点,
∴设P(x0,
x02+
),
抛物线E:x2=4y的准线方程l0为y=-1.
∵点P在直线l0上的射影为Q,
∴PQ=
x02+
,
∵M(0,2),∴PM=
=
x02+
,
∴PQ=PM.
(2)证明:由题设知直线AB的斜率一定存在,设AB:y=kx+2,
由
,得x2-4kx-8=0,
设A(x1,y1),B(x2,y2),则
x1+x2=4k,x1•x2=-8,
y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4=-8k2+8k2+4=4,
∵
=(x1,y1),
=(x2,y2),
∴
•
=x1x2+y1y2=-8+4=-4.
故
•
为定值-4.
(3)∵A(x1,y1),B(x2,y2),O(0,0),
∴直线AO:
=
,直线BO:
=
,
∵C,D都在直线l0:y=-1上,
∴C(-
,-1),D(-
,-1),
∴CD=|
-
|=
=
=
=
=
=2
,
∴当k=0时,CD取最小值2
.
| 1 |
| 6 |
| 1 |
| 2 |
∴设P(x0,
| 1 |
| 6 |
| 1 |
| 2 |
抛物线E:x2=4y的准线方程l0为y=-1.
∵点P在直线l0上的射影为Q,
∴PQ=
| 1 |
| 6 |
| 3 |
| 2 |
∵M(0,2),∴PM=
(x0-0)2+(
|
| 1 |
| 6 |
| 3 |
| 2 |
∴PQ=PM.
(2)证明:由题设知直线AB的斜率一定存在,设AB:y=kx+2,
由
|
设A(x1,y1),B(x2,y2),则
x1+x2=4k,x1•x2=-8,
y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4=-8k2+8k2+4=4,
∵
| OA |
| OB |
∴
| OA |
| OB |
故
| OA |
| OB |
(3)∵A(x1,y1),B(x2,y2),O(0,0),
∴直线AO:
| y |
| x |
| y1 |
| x1 |
| y |
| x |
| y2 |
| x2 |
∵C,D都在直线l0:y=-1上,
∴C(-
| x2 |
| y2 |
| x1 |
| y1 |
∴CD=|
| x2 |
| y2 |
| x1 |
| y1 |
| |x2y1-x1y2| |
| y1y2 |
=
| |x2(kx1+2)-x1(kx2+2)| |
| 4 |
=
| |x1-x2| |
| 2 |
| ||
| 2 |
=
| ||
| 2 |
| k2+2 |
∴当k=0时,CD取最小值2
| 2 |
点评:本题考查直线与抛物线的位置关系的应用,考查运算求解能力,推理论证能力;考查化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
 字词句段篇系列答案
字词句段篇系列答案
相关题目
 已知抛物线E的顶点在原点,焦点F在y轴正半轴上,抛物线上一点P(m,4)到其准线的距离为5,过点F的直线l依次与抛物线E及圆x2+(y-1)2=1交于A、C、D、B四点.
已知抛物线E的顶点在原点,焦点F在y轴正半轴上,抛物线上一点P(m,4)到其准线的距离为5,过点F的直线l依次与抛物线E及圆x2+(y-1)2=1交于A、C、D、B四点.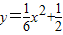 上任意一点,点P在直线l上的射影为Q,求证:PQ=PM;
上任意一点,点P在直线l上的射影为Q,求证:PQ=PM;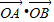 为定值;
为定值;