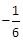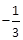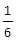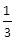题目内容
(1)若函数 在
在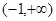 上是减函数,则
上是减函数,则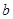 的取值范围是( )
的取值范围是( )
(2)已知函数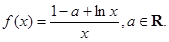 .则有
.则有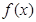 的极大值为________.
的极大值为________.
 在
在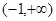 上是减函数,则
上是减函数,则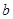 的取值范围是( )
的取值范围是( )A.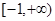 | B.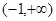 | C.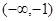 | D.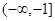 |
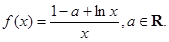 .则有
.则有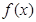 的极大值为________.
的极大值为________.(1)D;(2)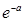 .
.
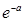 .
.试题分析:(1)先对函数进行求导,根据导函数小于0时即
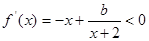 ,在
,在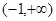 上恒成立,即
上恒成立,即 在
在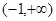 上恒成立,再由
上恒成立,再由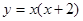 在
在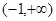 上是增函数且
上是增函数且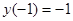 ,所以
,所以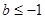 ;(2)先对函数求导,通过探讨导数的符号得函数的单调性,即可的函数的极大值.
;(2)先对函数求导,通过探讨导数的符号得函数的单调性,即可的函数的极大值.
练习册系列答案
相关题目
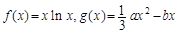 ,其中a,b∈R
,其中a,b∈R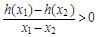 成立,试用a表示出b的取值范围;
成立,试用a表示出b的取值范围;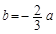 时,若
时,若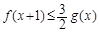 对x∈[0,+∞)恒成立,求a的最小值.
对x∈[0,+∞)恒成立,求a的最小值.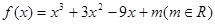 .
.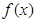 的极值(用含
的极值(用含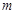 的式子表示);
的式子表示);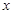 轴有3个不同交点,求
轴有3个不同交点,求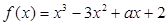 ,曲线
,曲线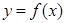 在点
在点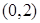 处的切线与
处的切线与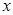 轴交点的横坐标为
轴交点的横坐标为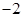 .
.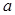 ;
;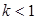 时,曲线
时,曲线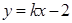 只有一个交点.
只有一个交点.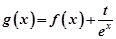 ,且A(x1,y1)、B(x2,y2)(x1≠x2)是曲线y=g(x)上任意两点,若对任意的t≤-1,直线AB的斜率恒大于常数m,求m的取值范围;
,且A(x1,y1)、B(x2,y2)(x1≠x2)是曲线y=g(x)上任意两点,若对任意的t≤-1,直线AB的斜率恒大于常数m,求m的取值范围;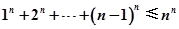 (n∈N*).
(n∈N*).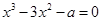 有三个不同的实数解,则a的取值范围是__________.
有三个不同的实数解,则a的取值范围是__________.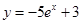 在点
在点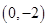 处的切线方程为________.
处的切线方程为________.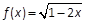 ,则
,则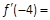 ( ).
( ).