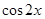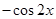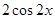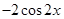题目内容
已知函数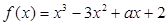 ,曲线
,曲线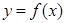 在点
在点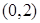 处的切线与
处的切线与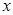 轴交点的横坐标为
轴交点的横坐标为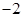 .
.
(1)求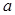 ;
;
(2)证明:当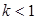 时,曲线
时,曲线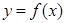 与直线
与直线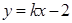 只有一个交点.
只有一个交点.
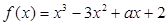 ,曲线
,曲线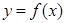 在点
在点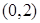 处的切线与
处的切线与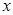 轴交点的横坐标为
轴交点的横坐标为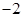 .
.(1)求
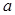 ;
;(2)证明:当
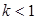 时,曲线
时,曲线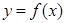 与直线
与直线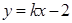 只有一个交点.
只有一个交点.(1)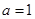 ;(2)详见解析.
;(2)详见解析.
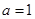 ;(2)详见解析.
;(2)详见解析.试题分析:(1)
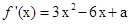 ,由导数的几何意义得
,由导数的几何意义得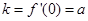 ,故切线方程为
,故切线方程为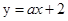 ,将点
,将点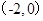 代入求
代入求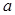 ;(2)曲线
;(2)曲线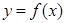 与直线
与直线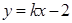 只有一个交点转化为函数
只有一个交点转化为函数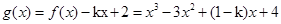 有且只有零点.一般思路往往利用导数求函数的单调区间和极值点,从而判断函数大致图象,再说明与
有且只有零点.一般思路往往利用导数求函数的单调区间和极值点,从而判断函数大致图象,再说明与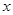 轴只有一个交点.本题首先入手点为
轴只有一个交点.本题首先入手点为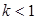 ,当
,当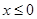 时,
时,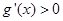 ,且
,且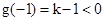 ,
,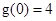 ,所以
,所以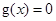 在
在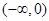 有唯一实根.只需说明当
有唯一实根.只需说明当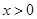 时无根即可,因为
时无根即可,因为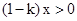 ,故只需说明
,故只需说明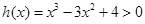 ,进而转化为求函数
,进而转化为求函数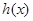 的最小值问题处理.
的最小值问题处理.(1)
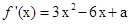 ,
,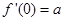 .曲线
.曲线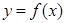 在点
在点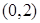 处的切线方程为
处的切线方程为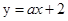 .由题设得,
.由题设得,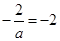 ,所以
,所以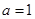 .
.(2)由(1)得,
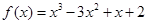 .设
.设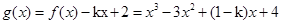 .由题设得
.由题设得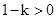 .当
.当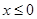 时,
时,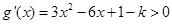 ,
,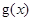 单调递增,
单调递增,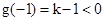 ,
,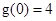 ,所以
,所以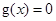 在
在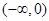 有唯一实根.当
有唯一实根.当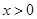 时,令
时,令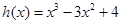 ,则
,则 .
.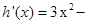
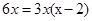 ,
,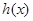 在
在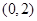 单调递减;在
单调递减;在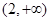 单调递增.所以
单调递增.所以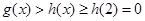 .所以
.所以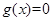 在
在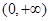 没有实根,综上,
没有实根,综上,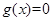 在
在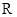 上有唯一实根,即曲线
上有唯一实根,即曲线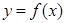 与直线
与直线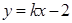 只有一个交点.
只有一个交点.
练习册系列答案
 开心练习课课练与单元检测系列答案
开心练习课课练与单元检测系列答案 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案
相关题目
 ,
, 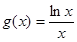 ,
,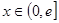 ,其中e是无理数且e="2.71828" ,
,其中e是无理数且e="2.71828" ,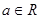 .
.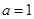 ,求
,求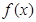 的单调区间与极值;
的单调区间与极值;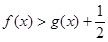 ;
;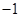 ?若存在,求出a的值;若不存在,说明理由.
?若存在,求出a的值;若不存在,说明理由. ,设
,设 为
为 的导数,
的导数,
 的值;
的值; 都成立.
都成立.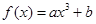 在
在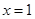 处的切线方程是
处的切线方程是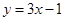 .
.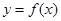 的解析式;
的解析式;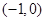 的切线方程.
的切线方程. 的导函数
的导函数 的图像如图所示,那么
的图像如图所示,那么

 在
在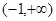 上是减函数,则
上是减函数,则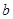 的取值范围是( )
的取值范围是( )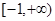
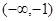
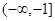
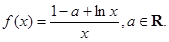 .则有
.则有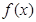 的极大值为________.
的极大值为________.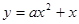 在点
在点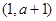 处的切线平行于
处的切线平行于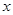 轴,则
轴,则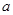 =_____________;
=_____________;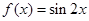 ,则
,则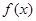 的导函数
的导函数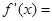 ( )
( )