题目内容
9.已知点H为△ABC的垂心,且$\overrightarrow{HA}$$•\overrightarrow{HB}$=-3,则$\overrightarrow{BH}$$•\overrightarrow{HC}$的值为3.分析 利用H为△ABC的垂心,所以AB⊥HC,BC⊥HA,AC⊥HB,然后利用向量表示垂直,用HA,HB,HC对应的向量表示,得到所求.
解答 解:因为H为△ABC的垂心,所以AB⊥HC,BC⊥HA,AC⊥HB,
所以$\overrightarrow{AB}•\overrightarrow{HC}=(\overrightarrow{HB}-\overrightarrow{HA})\overrightarrow{HC}=0$,所以$\overrightarrow{HB}•\overrightarrow{HC}=\overrightarrow{HA}•\overrightarrow{HC}$;
同理$\overrightarrow{HC}•\overrightarrow{HA}=\overrightarrow{HB}•\overrightarrow{HA}$,由$\overrightarrow{HA}$$•\overrightarrow{HB}$=-3,
所以 $\overrightarrow{BH}$$•\overrightarrow{HC}$=3;
故答案为:3.
点评 本题考查了三角形的垂心的性质以及平面向量垂直的性质;关键是由垂心得到$\overrightarrow{AB}•\overrightarrow{HC}=(\overrightarrow{HB}-\overrightarrow{HA})\overrightarrow{HC}=0$.

练习册系列答案
相关题目
1.已知不等式x2-2ax+a<0的解集为∅,则实数a的取值范围是( )
| A. | [0,1] | B. | (0,1] | C. | [0,1) | D. | (0,1) |
18.已知函数f(x)的定义域为R,且f(x)=f(-x),f(x+1)=-f(x),若f(x)在[-3,-2]上是减函数,$\frac{π}{4}$<α<β<$\frac{π}{2}$,则( )
| A. | f(sinα)>f(sinβ) | B. | f(cosα)>f(cosβ) | C. | f(tanα)>f(tanβ) | D. | 以上都不对 |
18.已知集合A=﹛-3,0,3﹜,B=﹛x|x2-2x-3=0﹜,则A∩B=( )
| A. | ∅ | B. | {3} | C. | {0} | D. | {-2} |
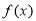 满足
满足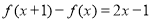 ,且
,且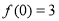 .
.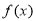 的解析式;
的解析式;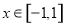 时,
时,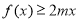 恒成立,求实数
恒成立,求实数 的取值集合.
的取值集合. 如图,在长方形ABCD中,对角线AC与两邻边所成的角分别为α、β,则cos2α+cos2β=1,则在立体几何中,给出类比猜想.
如图,在长方形ABCD中,对角线AC与两邻边所成的角分别为α、β,则cos2α+cos2β=1,则在立体几何中,给出类比猜想.