题目内容
已知函数f(x)=x2-(a+2)x+alnx(a∈R)。
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若a=4,y=f(x)的图像与直线y=m有三个交点,求m的取值范围。
(Ⅰ)求函数f(x)的单调区间;
(Ⅱ)若a=4,y=f(x)的图像与直线y=m有三个交点,求m的取值范围。
(1)见解析;(2)(4ln2-8,-5).
本试题主要考查了导数在研究函数中的运用,求解函数图像的交点问题的综合问题。
解:(Ⅰ)函数f(x)=x2-(a+2)x+alnx的定义域为(0,+∞),
f'(x)=2x-(a+2)+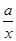 =
= 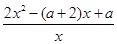 =
=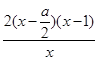
① 当a≤0时,f'(x)≤0在(0,1]上恒成立,f'(x)≥0在[1,+∞)上恒成立,
∴a≤0时,f(x)的增区间为[1,+∞),f(x)的减区间为(0,1]。
② 当0<a<2时,f'(x)≥0在(0,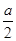 ]和[1,+∞)上恒成立,f'(x)≤0在[
]和[1,+∞)上恒成立,f'(x)≤0在[ 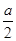 ,1]上恒成立.
,1]上恒成立.
∴0<a<2时,f(x)的增区间为(0,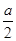 ]和[1,+∞),f(x)的减区间为[
]和[1,+∞),f(x)的减区间为[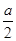 ,1].
,1].
③ a=2时,f'(x)≥0在(0,+∞)上恒成立,
∴a=2时,f(x)的增区间为(0,+∞).
④ a>2时,f'(x)≥0在(0,1]和[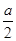 ,+∞)上恒成立,f'(x)≤0在[1,
,+∞)上恒成立,f'(x)≤0在[1, 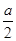 ]上恒成立,
]上恒成立,
∴a>2时,f(x)的增区间为(0,1]和[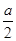 ,+∞),f(x)的减区间为[1,
,+∞),f(x)的减区间为[1, 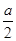 ].
].
(Ⅱ)若a=4,由(Ⅰ)可得f(x)在(0,1]上单调递增,在[1,2]上单调递减,在[2,+∞)上单调递增.
f(x)极小值=f(2)=4ln2-8, f(x)极大值=f(1)=-5,
∴y=f(x)的图像与直线y=m有三个交点时m的取值范围是(4ln2-8,-5)。
解:(Ⅰ)函数f(x)=x2-(a+2)x+alnx的定义域为(0,+∞),
f'(x)=2x-(a+2)+
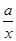 =
= 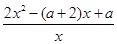 =
=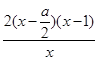
① 当a≤0时,f'(x)≤0在(0,1]上恒成立,f'(x)≥0在[1,+∞)上恒成立,
∴a≤0时,f(x)的增区间为[1,+∞),f(x)的减区间为(0,1]。
② 当0<a<2时,f'(x)≥0在(0,
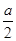 ]和[1,+∞)上恒成立,f'(x)≤0在[
]和[1,+∞)上恒成立,f'(x)≤0在[ 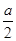 ,1]上恒成立.
,1]上恒成立.∴0<a<2时,f(x)的增区间为(0,
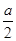 ]和[1,+∞),f(x)的减区间为[
]和[1,+∞),f(x)的减区间为[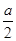 ,1].
,1].③ a=2时,f'(x)≥0在(0,+∞)上恒成立,
∴a=2时,f(x)的增区间为(0,+∞).
④ a>2时,f'(x)≥0在(0,1]和[
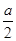 ,+∞)上恒成立,f'(x)≤0在[1,
,+∞)上恒成立,f'(x)≤0在[1, 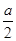 ]上恒成立,
]上恒成立,∴a>2时,f(x)的增区间为(0,1]和[
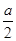 ,+∞),f(x)的减区间为[1,
,+∞),f(x)的减区间为[1, 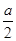 ].
].(Ⅱ)若a=4,由(Ⅰ)可得f(x)在(0,1]上单调递增,在[1,2]上单调递减,在[2,+∞)上单调递增.
f(x)极小值=f(2)=4ln2-8, f(x)极大值=f(1)=-5,
∴y=f(x)的图像与直线y=m有三个交点时m的取值范围是(4ln2-8,-5)。

练习册系列答案
相关题目

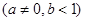 ,在区间
,在区间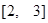 上有最大值4,最小值1,设函数
上有最大值4,最小值1,设函数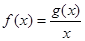 .
.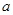 、
、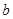 的值及函数
的值及函数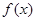 的解析式;
的解析式;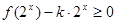 在
在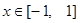 时恒成立,求实数
时恒成立,求实数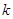 的取值范围;
的取值范围;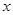 的方程
的方程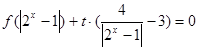 有三个相异的实数根,求实数
有三个相异的实数根,求实数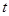 的取值范围.
的取值范围.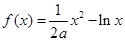 ,其中
,其中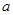 为大于零的常数.
为大于零的常数.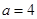 时,求函数
时,求函数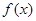 的单调区间和极值;
的单调区间和极值;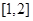 上至少存在一点
上至少存在一点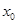 ,使得
,使得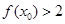 成立,求
成立,求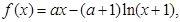 其中
其中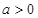 ,
,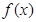 的单调区间;
的单调区间;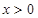 时,证明不等式:
时,证明不等式: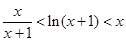 .
.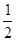 +
+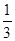 +
+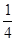 +L
+L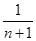 (
( ).
).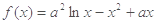 ,
,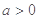
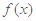 的定义域; (Ⅱ)求
的定义域; (Ⅱ)求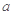 ,使
,使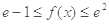 对
对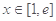 恒成立.
恒成立.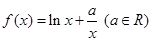
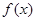 的单调性;
的单调性;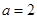 时,求函数
时,求函数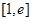 上的最值.
上的最值.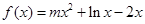 .
.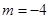 ,求函数
,求函数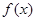 的最大值.
的最大值.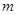 的取值范围
的取值范围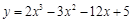 在[0,3]上的最大值和最小值分别是( ).
在[0,3]上的最大值和最小值分别是( ).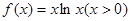 的单调递增区间是
的单调递增区间是