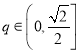题目内容
【题目】已知 n 个四元集合 A1 , A2 ,…, An ,每两个有且只有一个公共元 ,并且有Card(A1 ∪ A2 ∪ …∪ An)=n .试求 n 的最大值.这里 Card A 为集合A中元素的个数 .
【答案】13
【解析】
考虑任一元![]() .
.
如果每个 Ai 均含有a , 则由条件知, 各 Ai 中的其他元素都不相同.
故![]() ,与已知条件相违.
,与已知条件相违.
因此, 必有一个 Ai 不含a .
不妨设 a![]() A1 .若含 a 的集合大于或等于 5个, 那么, 由已知条件得知 A1与这 5个集合各有一个公共元(此元当然不等于a), 而且这 5个元互不相同(若相同, 则这个公共元是2个含 a 的集合的公共元 , 于是, 这两个集合就有 2 个公共元, 又与已知条件相违), 从而, Card A1≥5, 矛盾.所以 , 含a的集合小于或等于 4 个.
A1 .若含 a 的集合大于或等于 5个, 那么, 由已知条件得知 A1与这 5个集合各有一个公共元(此元当然不等于a), 而且这 5个元互不相同(若相同, 则这个公共元是2个含 a 的集合的公共元 , 于是, 这两个集合就有 2 个公共元, 又与已知条件相违), 从而, Card A1≥5, 矛盾.所以 , 含a的集合小于或等于 4 个.
另一方面, 因为![]() ,所以, 每个元恰好属于 4个集合.
,所以, 每个元恰好属于 4个集合.
不妨设含有元 b 的集合为 A1 、A2 、A3 、A4.
由上述的结论可知![]() .
.
如果 n >13, 那么, 存在元 c![]() A1∪A2∪A3∪A4.设含 c 的集合为 A5, 则 A5不是
A1∪A2∪A3∪A4.设含 c 的集合为 A5, 则 A5不是![]() .因而, 不含 b .而 A5与
.因而, 不含 b .而 A5与![]() 各有一个公共元(当然不是 b), 这 4个公共元互不相同(理由同上), 又都不是 c , 从而,
各有一个公共元(当然不是 b), 这 4个公共元互不相同(理由同上), 又都不是 c , 从而,![]() , 矛盾.
, 矛盾.
因此, n ≤13.
n ≤13 是可能的.例如, 不难验证, 如下的13个集合符合要求.
{0, 1, 2, 3},{0, 4, 5, 6},{0, 7, 8, 9},{0, 10, 11, 12},{10, 1, 4, 7}, {10, 2, 5, 8}, {10, 3, 6, 9},{11, 1, 5, 9},{11, 2, 6, 7}, {11, 3, 4, 8}, {12, 1, 6, 8},{12, 2, 4, 9},{12, 3, 5, 7}.
故 n 的最大值为13.