Question

【题目】已知命题 “存在”，命题：“曲线表示焦点在轴上的椭圆”，命题 “曲线表示双曲线”

（1）若“且”是真命题，求实数的取值范围；

（2）若是的必要不充分条件，求实数的取值范围.

Answer 1

【答案】（1）或（2）或

【解析】试题分析：（1）若“p且q”是真命题，则p，q同时为真命题，建立条件关系，即可求m的取值范围；
（2）根据q是s的必要不充分条件，建立条件关系，即可求t的取值范围．

试题解析：

(Ⅰ)解：若p为真，则

解得：m≤－1或m≥3

若q为真，则

解得：－4 < m < －2或m > 4

若“p且q”是真命题，则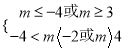

解得： 或m > 4

∴m的取值范围是{ m |或m > 4}

(Ⅱ)解：若s为真，则，即t < m < t + 1

∵由q是s的必要不充分条件

∴

即或t≥4

解得： 或t≥4

∴t的取值范围是{ t |或t≥4}