题目内容
(本小题满分13分)
设椭圆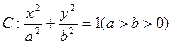 的离心率
的离心率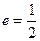 ,右焦点到直线
,右焦点到直线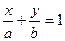 的距离
的距离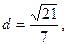
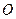 为坐标原点.
为坐标原点.
(I)求椭圆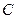 的方程;
的方程;
(II)过点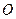 作两条互相垂直的射线,与椭圆
作两条互相垂直的射线,与椭圆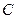 分别交于
分别交于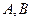 两点,证明点
两点,证明点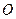 到直
到直
线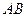 的距离为定值,并求弦
的距离为定值,并求弦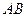 长度的最小值.
长度的最小值.
设椭圆
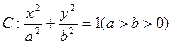 的离心率
的离心率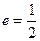 ,右焦点到直线
,右焦点到直线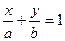 的距离
的距离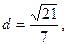
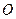 为坐标原点.
为坐标原点.(I)求椭圆
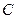 的方程;
的方程;(II)过点
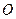 作两条互相垂直的射线,与椭圆
作两条互相垂直的射线,与椭圆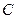 分别交于
分别交于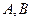 两点,证明点
两点,证明点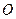 到直
到直线
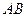 的距离为定值,并求弦
的距离为定值,并求弦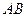 长度的最小值.
长度的最小值.(Ⅰ)
(Ⅱ)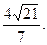

(Ⅱ)
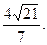
(Ⅰ)由
由右焦点到直线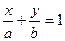 的距离为
的距离为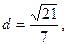
得: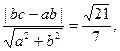 解得
解得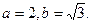
所以椭圆C的方程为 …………4分
…………4分
(Ⅱ)设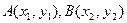 ,
,
直线AB的方程为
与椭圆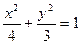 联立消去y得
联立消去y得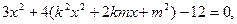
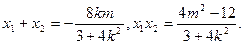
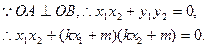
即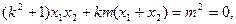
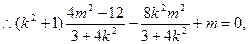
整理得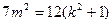 所以O到直线AB的距离
所以O到直线AB的距离
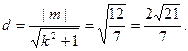 …………8分
…………8分
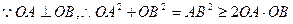 , 当且仅当OA=OB时取“=”号。
, 当且仅当OA=OB时取“=”号。
由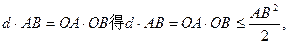
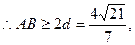
即弦AB的长度的最小值是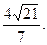 …………13分
…………13分

由右焦点到直线
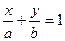 的距离为
的距离为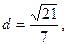
得:
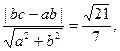 解得
解得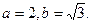
所以椭圆C的方程为
 …………4分
…………4分(Ⅱ)设
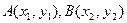 ,
,直线AB的方程为

与椭圆
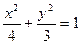 联立消去y得
联立消去y得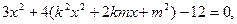
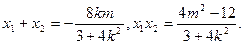
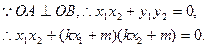
即
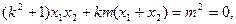
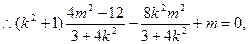
整理得
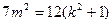 所以O到直线AB的距离
所以O到直线AB的距离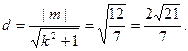 …………8分
…………8分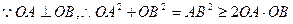 , 当且仅当OA=OB时取“=”号。
, 当且仅当OA=OB时取“=”号。由
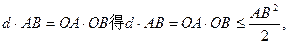
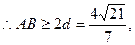
即弦AB的长度的最小值是
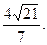 …………13分
…………13分
练习册系列答案
相关题目
 的直线
的直线 分别与
分别与 正半轴,
正半轴,  轴正半轴交于
轴正半轴交于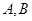 两点,
两点, 为坐标原点,则三角形
为坐标原点,则三角形 面积最小时直线方程为
面积最小时直线方程为  、
、 ,(
,( )是曲线C上的两点,点
)是曲线C上的两点,点 、
、 关于
关于 轴对称,直线
轴对称,直线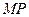 、
、 分别交
分别交 和点
和点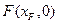 ,
, 、
、 、
、 、
、 分别表示
分别表示 和
和 ;
;  时,
时, 是一个定值与点
是一个定值与点 的位置无关;请你试探究当曲线C的方程为:
的位置无关;请你试探究当曲线C的方程为: 时,
时,  的值是否也与点M、N、P的位置无关;
的值是否也与点M、N、P的位置无关; 时,探究
时,探究 与
与 经加、减、乘、除的某一种运算后为定值的一个正确结论.(只要求写出你的探究结论,无须证明).
经加、减、乘、除的某一种运算后为定值的一个正确结论.(只要求写出你的探究结论,无须证明).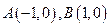 ,过曲线
,过曲线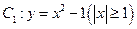 上一点
上一点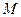 的切线
的切线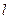 ,与曲线
,与曲线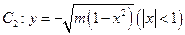 也相切于点
也相切于点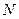 ,记点
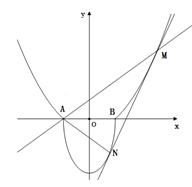
,记点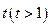 。
。
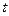 表示切线
表示切线 的值和点
的值和点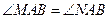 ?
?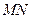 所在直线的方程。
所在直线的方程。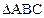 的三个顶点是
的三个顶点是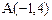 ,
,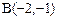 ,
,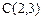 .
.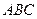 的重心
的重心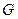 任作一直线分别交
任作一直线分别交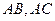 于
于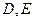 ,
,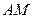 为中线
为中线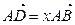 ,
,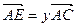 ,
,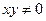 ,求
,求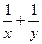 的值
的值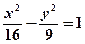 上到定点
上到定点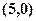 的距离是
的距离是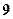 的点的个数是( )
的点的个数是( ) 个
个 个
个 个
个 个
个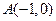 、
、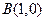 两定点,且以圆
两定点,且以圆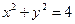 的任一条切线
的任一条切线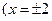 除外)为准线,则该抛物线的焦点F的轨迹方程为: ;
除外)为准线,则该抛物线的焦点F的轨迹方程为: ;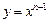 (
(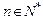 )在点
)在点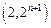 处的切线与
处的切线与 轴交点的横坐标为
轴交点的横坐标为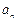 ,则
,则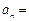 .
.