题目内容
4．若a=$\frac{l{n}^{2}6}{4}$，b=ln2×ln3，c=$\frac{l{n}^{2}2π}{4}$，则a，b，c的大小关系是b＜a＜c．分析 先对b利用基本不等式可比较b与a的大小，然后根据对数函数的单调性可判定a与c的大小，即可的答案．
解答 解：∵b=ln2×ln3＜$（\frac{ln2+ln3}{2}）^{2}$=$\frac{l{n}^{2}6}{4}$=a，
∵1＜ln6＜ln2π
∴a=$\frac{l{n}^{2}6}{4}$＜$\frac{l{n}^{2}2π}{4}$=c
∴b＜a＜c
故答案为：b＜a＜c．
点评 本题考查不等式比较大小，涉及基本不等式和对数函数的单调性，属基础题．
练习册系列答案
相关题目
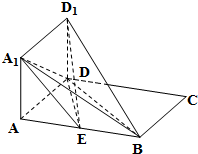如图所示，正方形AA1D1D与矩形ABCD所在平面互相垂直，AB=2AD=2，点E为AB的中点．求直线D1E与平面A1D1B所成角的正弦值．
从某班的科技创新比赛结果中任抽取9名学生的成绩，其分布如茎叶图所示：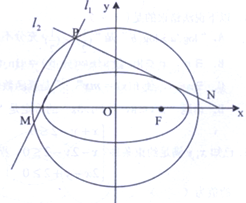
已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个焦点F（$\sqrt{2}$，0）其短轴上的一个端点到F的距离为$\sqrt{3}$
13．设a为实常数，y=f（x）是定义在R上的奇函数，当x＞0时，f（x）=4x+$\frac{1}{x}$+3，则对于y=f（x）在x＜0时，下列说法正确的是（ ）
| A． | 有最大值7 | B． | 有最大值-7 | C． | 有最小值7 | D． | 有最小值-7 |
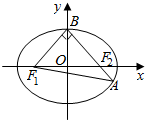如图，在平面直角坐标系xOy中，椭圆C：$\frac{x^2}{a^2}+\frac{y^2}{b^2}$=1（a＞b＞0）的左右焦点分别为，F1和F2，上顶点为B，BF2，延长线交椭圆于点A，△ABF的周长为8，且$\overrightarrow{B{F_1}}•\overrightarrow{BA}$=0．