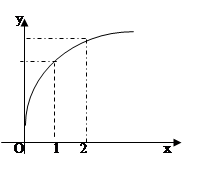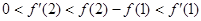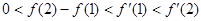题目内容
对于在区间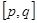 上有意义的两个函数
上有意义的两个函数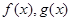 ,如果对于任意的
,如果对于任意的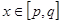 ,都有
,都有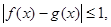 则称
则称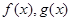 在区间
在区间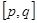 上是“接近的”两个函数,否则称它们在区间
上是“接近的”两个函数,否则称它们在区间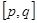 上是“非接近的”两个函数。现有两个函数
上是“非接近的”两个函数。现有两个函数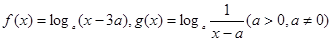 给定一个区间
给定一个区间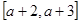 。
。
(1)若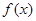 在区间
在区间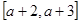 有意义,求实数
有意义,求实数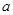 的取值范围;
的取值范围;
(2)讨论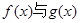 在区间
在区间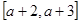 上是否是“接近的”。
上是否是“接近的”。
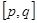 上有意义的两个函数
上有意义的两个函数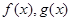 ,如果对于任意的
,如果对于任意的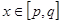 ,都有
,都有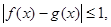 则称
则称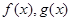 在区间
在区间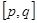 上是“接近的”两个函数,否则称它们在区间
上是“接近的”两个函数,否则称它们在区间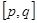 上是“非接近的”两个函数。现有两个函数
上是“非接近的”两个函数。现有两个函数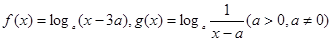 给定一个区间
给定一个区间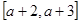 。
。(1)若
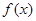 在区间
在区间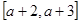 有意义,求实数
有意义,求实数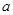 的取值范围;
的取值范围;(2)讨论
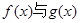 在区间
在区间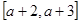 上是否是“接近的”。
上是否是“接近的”。(1) (2)当
(2)当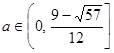 时,
时, 与
与 是接近的
是接近的
 (2)当
(2)当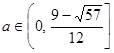 时,
时, 与
与 是接近的
是接近的试题分析:(1)要使
 有意义,则有
有意义,则有
要使
 在
在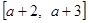 上有意义,等价于真数的最小值大于0
上有意义,等价于真数的最小值大于0即

(2)
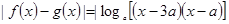 , 令
, 令 ,
,得
 。(*)
。(*)因为
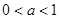 ,所以
,所以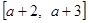 在直线
在直线 的右侧。
的右侧。所以
 在
在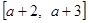 上为减函数。
上为减函数。所以
 。
。于是
 ,∴
,∴ 。
。所以当
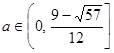 时,
时, 与
与 是接近的
是接近的点评:第一小题函数定义域要满足使函数有意义,第二小题的求解首先要理解函数是接近的其实质是最值在
 指间,进而转化为求函数
指间,进而转化为求函数 的最值
的最值
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
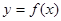 在R是奇函数,且当
在R是奇函数,且当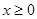 时,
时,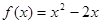 ,则
,则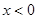 时,
时,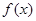 的解析式为____ ___________
的解析式为____ ___________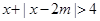 恒成立,则实数
恒成立,则实数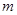 的取值范围是:_ .
的取值范围是:_ .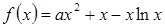 ,
,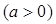
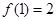 ,且在定义域内
,且在定义域内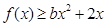 恒成立,求实数
恒成立,求实数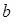 的取值范围;
的取值范围;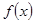 在定义域上是单调函数,求实数
在定义域上是单调函数,求实数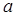 的取值范围;
的取值范围; .
.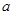 的值,使
的值,使 为奇函数;
为奇函数;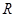 上的奇函数
上的奇函数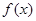 满足
满足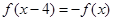 ,且在区间
,且在区间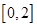 上是增函数,则当
上是增函数,则当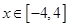 时,不等式
时,不等式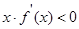 的解集为( )
的解集为( )

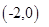

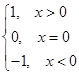 , g(x)=
, g(x)=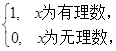 则f(g(
则f(g(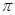 ))的值为( )
))的值为( )  ,则( )
,则( )



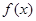 的图象如图所示,下列数值排序正确的是
的图象如图所示,下列数值排序正确的是