题目内容
【题目】定义在![]() 上的函数
上的函数![]() 满足
满足![]() ,当
,当![]() 时,
时, ,函数
,函数![]() .若对任意
.若对任意![]() ,存在
,存在![]() ,不等式
,不等式![]() 成立,则实数
成立,则实数![]() 的取值范围是( )
的取值范围是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】A
【解析】分析:先求出函数f(x)在![]() 的值域,再根据
的值域,再根据![]() ,求出函数f(x)在x
,求出函数f(x)在x![]() 时的值域和最小值,再利用导数求函数g(x)的最小值即得解.
时的值域和最小值,再利用导数求函数g(x)的最小值即得解.
详解:由题得函数![]() 在[0,1]上的值域为
在[0,1]上的值域为![]() ,
,
函数![]()
![]() 在[1,
在[1,![]() 上是减函数,在
上是减函数,在![]() 上是增函数,
上是增函数,
所以函数在![]() 上的值域为
上的值域为![]() .
.
所以函数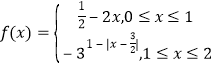 在
在![]() 的值域为
的值域为![]() ∪
∪![]() .
.
因为定义在![]() 上的函数
上的函数![]() 满足
满足![]() ,
,
所以函数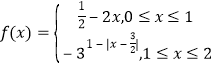 在
在![]() 的值域为
的值域为![]() ∪
∪![]() .
.
所以函数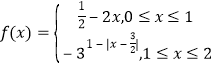 在
在![]() 的值域为
的值域为![]() ∪
∪![]() .
.
所以函数f(x)在![]() 的最小值为-12.
的最小值为-12.
∵函数g(x)=x3+3x2+m,
∴![]() =3x2+6x,
=3x2+6x,
令3x2+6x>0,所以x>0或x<﹣2,
令3x2+6x<0,所以﹣2<x<0,
∴函数g(x)=x3+3x2+m,在(﹣∞,﹣2),(0,+∞)单调递增.在(﹣2,0)单调递减,
∴t∈[﹣4,﹣2),g(t)最小=g(﹣4)=m﹣16,
∵不等式f(s)﹣g(t)≥0,
∴﹣12≥m﹣16,
故实数满足m≤4,
故答案为:A

练习册系列答案
相关题目


