题目内容
(1)双曲线与椭圆
+
=1有相同焦点,且经过点(
,4),求其方程.
(2)椭圆过两点(
,1),(-
,-
),求其方程.
| x2 |
| 27 |
| y2 |
| 36 |
| 15 |
(2)椭圆过两点(
| 6 |
| 3 |
| 2 |
(1)椭圆
+
=1中c=
=3,∴焦点为(0,±3),
设双曲线方程为
-
=1
∵双曲线过(
,4),则
-
=1,得a2=4或36,
而a2<9,
∴a2=4,
∴双曲线方程为
-
=1.
(2)设椭圆方程为Ax2+By2=1(A>0,B>),则
,∴A=
,B=
,
∴所求椭圆方程为
+
=1.
| x2 |
| 27 |
| y2 |
| 36 |
| 36-27 |
设双曲线方程为
| y2 |
| a2 |
| x2 |
| 9-a2 |
∵双曲线过(
| 15 |
| 16 |
| a2 |
| 15 |
| 9-a2 |
而a2<9,
∴a2=4,
∴双曲线方程为
| y2 |
| 4 |
| x2 |
| 5 |
(2)设椭圆方程为Ax2+By2=1(A>0,B>),则
|
| 1 |
| 9 |
| 1 |
| 3 |
∴所求椭圆方程为
| x2 |
| 9 |
| y2 |
| 3 |

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 在椭圆
在椭圆 的第一象限上运动
的第一象限上运动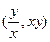 的轨迹
的轨迹 的方程
的方程 有最大值,试求椭圆
有最大值,试求椭圆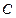 的离心率的取值范围。
的离心率的取值范围。