题目内容
(本小题满分14分)已知函数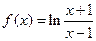
(Ⅰ)求函数的定义域,并证明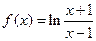 在定义域上是奇函数;
在定义域上是奇函数;
(Ⅱ)若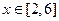
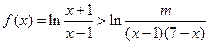 恒成立,求实数
恒成立,求实数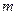 的取值范围;
的取值范围;
(Ⅲ)当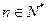 时,试比较
时,试比较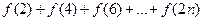 与
与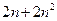 的大小关系.
的大小关系.
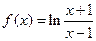
(Ⅰ)求函数的定义域,并证明
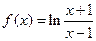 在定义域上是奇函数;
在定义域上是奇函数;(Ⅱ)若
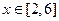
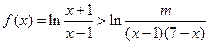 恒成立,求实数
恒成立,求实数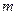 的取值范围;
的取值范围;(Ⅲ)当
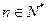 时,试比较
时,试比较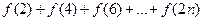 与
与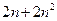 的大小关系.
的大小关系.(Ⅰ)函数的定义域为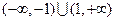 ,
,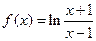 在定义域上是奇函数。
在定义域上是奇函数。
(Ⅱ)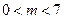
(Ⅲ)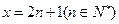 时,
时,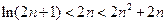 成立.
成立.
 ,
,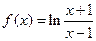 在定义域上是奇函数。
在定义域上是奇函数。(Ⅱ)
(Ⅲ)
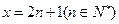 时,
时,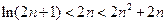 成立.
成立.解:(Ⅰ)由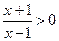 ,解得
,解得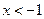 或
或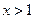 ,
,
∴ 函数的定义域为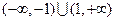 ………2分
………2分
当 时,
时,
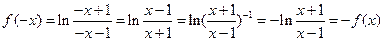
∴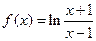 在定义域上是奇函数。 ………4分
在定义域上是奇函数。 ………4分
(Ⅱ)由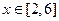 时,
时,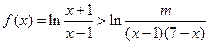 恒成立,
恒成立,
∴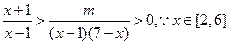
∴ 在
在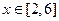 成立 ………6分
成立 ………6分
令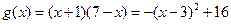 ,
,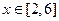 ,由二次函数的性质可知
,由二次函数的性质可知
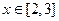 时函数单调递增,
时函数单调递增,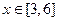 时函数单调递减,
时函数单调递减,
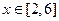 时,
时,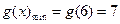
∴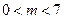 ………8分
………8分
(Ⅲ)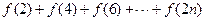 =
=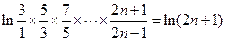 …9分
…9分
证法一:构造函数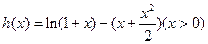 ,
,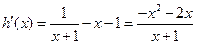
当 时,
时,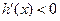 ,∴
,∴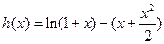 在
在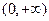 单调递减,
单调递减,
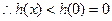 ………12分
………12分
当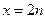 (
( )时,
)时,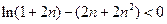
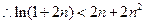 …14分
…14分
证法二:构造函数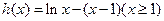 ,证明:
,证明: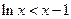 在
在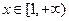 成立,则当
成立,则当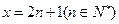 时,
时,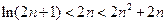 成立.
成立.
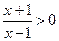 ,解得
,解得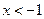 或
或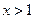 ,
,∴ 函数的定义域为
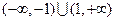 ………2分
………2分当
 时,
时,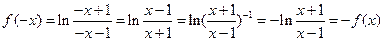
∴
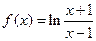 在定义域上是奇函数。 ………4分
在定义域上是奇函数。 ………4分(Ⅱ)由
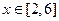 时,
时,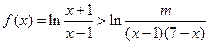 恒成立,
恒成立,∴
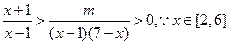
∴
 在
在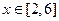 成立 ………6分
成立 ………6分令
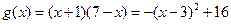 ,
,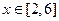 ,由二次函数的性质可知
,由二次函数的性质可知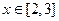 时函数单调递增,
时函数单调递增,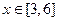 时函数单调递减,
时函数单调递减,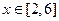 时,
时,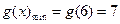
∴
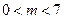 ………8分
………8分(Ⅲ)
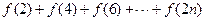 =
=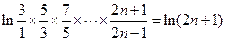 …9分
…9分证法一:构造函数
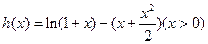 ,
,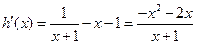
当
 时,
时, ,∴
,∴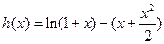 在
在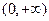 单调递减,
单调递减,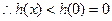 ………12分
………12分当
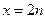 (
( )时,
)时,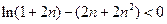
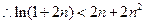 …14分
…14分证法二:构造函数
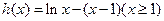 ,证明:
,证明: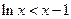 在
在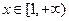 成立,则当
成立,则当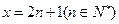 时,
时,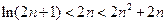 成立.
成立.
练习册系列答案
相关题目
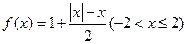
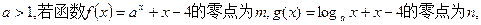
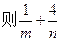 的取值范围是( )
的取值范围是( )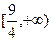

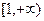
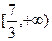
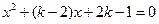 的两根中,一根在
的两根中,一根在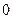 和
和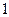 之间,另一根在
之间,另一根在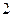 之间,则实数
之间,则实数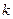 的取值范围是 ;
的取值范围是 ;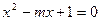 的两根为
的两根为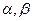 ,且
,且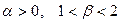 ,则实数的取值范围是________.
,则实数的取值范围是________. 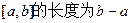 ,区间
,区间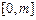 在映射
在映射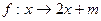 所得的对应区间为
所得的对应区间为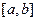 ,若区间
,若区间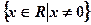 ;
;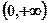 上为增函数.
上为增函数.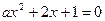 至少有一个负实根,则实数a的取值范( )
至少有一个负实根,则实数a的取值范( )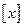 表示不超过实数
表示不超过实数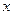 的最大整数,
的最大整数,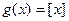 为取整函数,
为取整函数,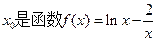 的零点,则
的零点,则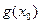 等于 ( )
等于 ( )