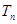题目内容
(本小题满分14分)
已知数列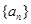 ,
,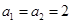 ,
,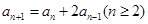
(Ⅰ)求数列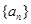 的通项公式
的通项公式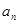 ;
;
(Ⅱ)当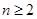 时,求证:
时,求证: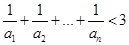
(Ⅲ)若函数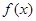 满足:
满足: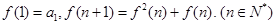
求证: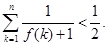
已知数列
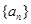 ,
,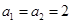 ,
,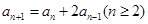
(Ⅰ)求数列
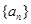 的通项公式
的通项公式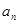 ;
;(Ⅱ)当
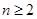 时,求证:
时,求证: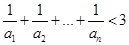
(Ⅲ)若函数
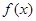 满足:
满足: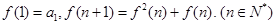
求证:
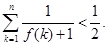
(1)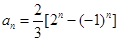 ;(2)见解析;(3)证明:见解析。
;(2)见解析;(3)证明:见解析。
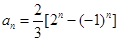 ;(2)见解析;(3)证明:见解析。
;(2)见解析;(3)证明:见解析。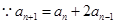 ,两边加
,两边加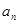 得:
得: 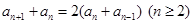 ,
,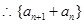 是以2为公比,
是以2为公比, 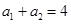 为首项的等比数列.
为首项的等比数列. 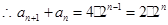 ---------①
---------① 由
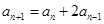 两边减
两边减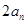 得:
得: 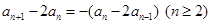
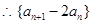 是以
是以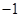 为公比,
为公比, 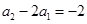 为首项的等比数列.
为首项的等比数列. 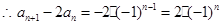 -----------②
-----------②①-②得:
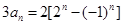 所以,所求通项为
所以,所求通项为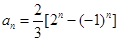
(2)当
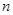 为偶数时,
为偶数时,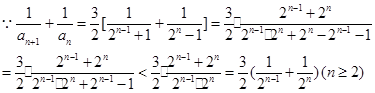
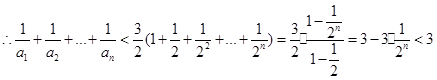
当
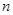 为奇数时,
为奇数时,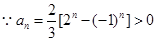 ,
,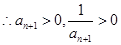 ,又
,又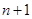 为偶数
为偶数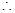 由(1)知,
由(1)知, 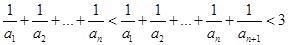
(3)证明:
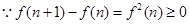
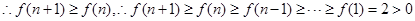
又
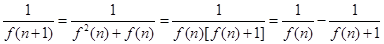
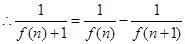
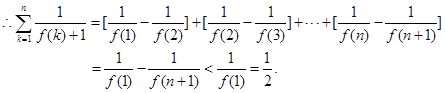

练习册系列答案
相关题目
 的前
的前 项和为
项和为 ,
, (
(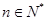 ).
). 是等比数列,求出数列
是等比数列,求出数列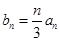 ,求数列
,求数列 的前
的前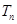 ;
;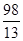
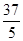
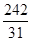

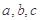 成等比数列,
成等比数列,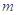 是
是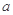 与
与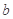 的等差中项,
的等差中项,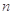 是
是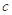 的等差中项,则
的等差中项,则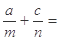 ( )
( )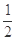
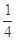
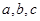 成等比数列,
成等比数列,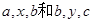 分别成等差数列,且
分别成等差数列,且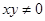 ,则
,则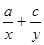 的值等于( )
的值等于( )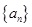 的前5项的和为30,前10项的和为100,则它的前15的和为( )
的前5项的和为30,前10项的和为100,则它的前15的和为( )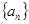 的前n项和
的前n项和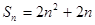 ,数列
,数列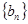 的前n项和
的前n项和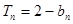 ,
,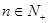 ,
,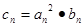 ,是否存在正整数
,是否存在正整数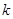 ,使得
,使得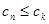 对
对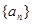 为等差数列,若
为等差数列,若 ,且它的前
,且它的前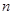 项和
项和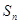 有最小值,那么当
有最小值,那么当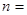
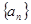 满足
满足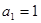 ,
,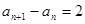 ;数列
;数列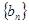 满足
满足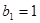 ,
,
 和
和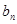 的通项公式
的通项公式 的前
的前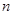 项和
项和