题目内容
14. 如图所示,PA为圆O的切线,A为切点,PO交圆O于B,C两点,PA=2,PB=1,∠BAC的角平分线与BC和圆O分别交于点D和E.
如图所示,PA为圆O的切线,A为切点,PO交圆O于B,C两点,PA=2,PB=1,∠BAC的角平分线与BC和圆O分别交于点D和E.(Ⅰ)求证:AB•PC=PA•AC;
(Ⅱ)求AD•AE的值.
分析 (Ⅰ)由已知条件推导出△PAB∽△PCA,由此能够证明AB•PC=PA•AC.
(Ⅱ)由切割线定理求出PC=4,BC=3,由已知条件条件推导出△ACE∽△ADB,由此能求出AD•AE的值.
解答 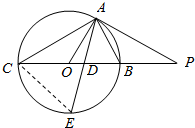 (Ⅰ)证明:∵PA为圆O的切线,
(Ⅰ)证明:∵PA为圆O的切线,
∴∠PAB=∠ACP,
又∠P为公共角
∴△PAB∽△PCA,
∴$\frac{AB}{AC}=\frac{PA}{PC}$,
∴AB•PC=PA•AC.…(4分)
(Ⅱ)解:∵PA为圆O的切线,BC是过点O的割线,
∴PA2=PB•PC,
∴PC=4,BC=3,
又∵∠CAB=90°,∴AC2+AB2=BC2=9,
又由(Ⅰ)知$\frac{AB}{AC}=\frac{PA}{PC}$=$\frac{1}{2}$,
∴AC=$\frac{6}{\sqrt{5}}$,AB=$\frac{3}{\sqrt{5}}$,
连接EC,则∠CAE=∠EAB,∠AEC=∠ABD
∴△ACE∽△ADB,∴$\frac{AB}{AE}=\frac{AD}{AC}$,
∴AD•AE=AB•AC=$\frac{18}{5}$.(10分)
点评 本题考查三角形相似的证明和应用,考查线段乘积的求法,是中档题,解题时要注意切割线定理的合理运用.

练习册系列答案
 名师点拨卷系列答案
名师点拨卷系列答案
相关题目
6. 一个大风车的半径为8m,12min旋转一周,它的最低点Po离地面2m,风车翼片的一个端点P从Po开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )
一个大风车的半径为8m,12min旋转一周,它的最低点Po离地面2m,风车翼片的一个端点P从Po开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )
 一个大风车的半径为8m,12min旋转一周,它的最低点Po离地面2m,风车翼片的一个端点P从Po开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )
一个大风车的半径为8m,12min旋转一周,它的最低点Po离地面2m,风车翼片的一个端点P从Po开始按逆时针方向旋转,则点P离地面距离h(m)与时间f(min)之间的函数关系式是( )| A. | $h(t)=-8sin\frac{π}{6}t+10$ | B. | $h(t)=-8cos\frac{π}{6}t+10$ | C. | $h(t)=-8sin\frac{π}{6}t+8$ | D. | $h(t)=-8cos\frac{π}{6}t+8$ |
5.在某次数学测试中,记答对题数:大于或等于6道为合格,小于6道为不合格,现从A,B两个班级随机抽取5人答对的题数进行分析,结果记录如下:
由于表格受损,数据m,n看不清,统计人员只记得m<n,且在抽取的数据中,A班的平均数比B班的平均数多1道题,两班数据的方差相同
(1)求表格中m和n的值;
(2)若从抽取的B班5人中任取2人,求2人都合格的概率.
| A班 | 5 | 5 | 8 | 8 | 9 |
| B班 | m | 4 | 7 | n | 8 |
(1)求表格中m和n的值;
(2)若从抽取的B班5人中任取2人,求2人都合格的概率.
2.若离散型随机变量X的分布列为 则X的数学期望E(X)=( )
| X | 0 | 1 |
| P | $\frac{a}{2}$ | $\frac{{a}^{2}}{2}$ |
| A. | 2 | B. | 2或$\frac{1}{2}$ | C. | $\frac{1}{2}$ | D. | 1 |
6.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的实轴长为2,离心率为$\sqrt{5}$,则它的一个焦点到它的一条渐近线的距离为( )
| A. | 1 | B. | 2 | C. | $\sqrt{5}$ | D. | 2$\sqrt{2}$ |
3.若函数f (x)=ex+4x-kx在区间($\frac{1}{2}$,+∞)上是增函数,则实数k的最大值是( )
| A. | 2+e | B. | 2+$\sqrt{e}$ | C. | 4+e | D. | 4ln2+$\sqrt{e}$ |
4.过椭圆$\frac{x^2}{25}+\frac{y^2}{16}$=1上一点P作圆(x-3)2+y2=1的两条切线,切点分别为A、B,则∠APB的最大值为( )
| A. | 30° | B. | 60° | C. | 90° | D. | 120° |