题目内容

4．过椭圆$\frac{x^2}{25}+\frac{y^2}{16}$=1上一点P作圆（x-3）2+y2=1的两条切线，切点分别为A、B，则∠APB的最大值为（　　）
A．30°B．60°C．90°D．120°

分析 画出图形，利用圆与椭圆的对称性，找出P的位置求解即可．

解答 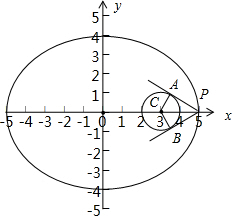解：如图：因为椭圆$\frac{x^2}{25}+\frac{y^2}{16}$=1与圆（x-3）2+y2=1的对称轴是x轴，并且圆的圆心坐标（3，0）为椭圆的右焦点，
所以过椭圆$\frac{x^2}{25}+\frac{y^2}{16}$=1上一点P作圆（x-3）2+y2=1的两条切线，切点分别为A、B，
则∠APB的最大值就是椭圆上的点到圆的圆心的距离最小值时的点，为右端点P，
圆的半径为1，AC=1，PC=2，AC⊥AP，∴∠APB=2∠APC=60°．
故选：C．

点评 本题考查椭圆与圆的综合应用，直线与圆的位置关系，考查数形结合以及椭圆的简单性质的应用．

练习册系列答案
相关题目
14．如图所示，PA为圆O的切线，A为切点，PO交圆O于B，C两点，PA=2，PB=1，∠BAC的角平分线与BC和圆O分别交于点D和E．
（Ⅰ）求证：AB•PC=PA•AC；
（Ⅱ）求AD•AE的值．
15．某公司采用招考的方式引进人才，规定考生必须在B、C、D三个测试点中任意选取两个进行测试，若在这两个测试点都测试合格，则可参加面试，否则不被录用．已知考生在每个测试点的测试结果只有合格与不合格两种，且在每个测试点的测试结果互不影响．若考生小李和小王一起前来参加招考，小李在测试点B、C、D测试合格的概率分别为$\frac{2}{3}$，$\frac{1}{3}$，$\frac{1}{2}$，小王在上述三个测试点测试合格的概率都是$\frac{2}{3}$．
（Ⅰ）问小李选择哪两个测试点测试才能使得可以参加面试的可能性最大？请说明理由；
（Ⅱ）假设小李选择测试点B、C进行测试，小王选择测试点B、D进行测试，记ξ为两人在各测试点测试合格的测试点个数之和，求随机变量ξ的分布列及数学期望Eξ．
12．设全集U=R，集合A={x|x2-3x-4＜0}，B={x|log2（x-1）＜2}，则A∩B=（1，4），A∪B=（-1，5），CRA=（-∞，-1]∪[4，+∞）．
19．设函数f（x）=sin（ωx+φ）（ω，φ是常数，ω＞0，0＜φ＜π），若f（x）在区间[$\frac{π}{6}$，$\frac{π}{3}$]上具有单调性，且f（$\frac{π}{6}$）=-f（$\frac{π}{3}$）=-f（$\frac{π}{2}$），则f（$\frac{π}{ω}$）的值为-$\frac{\sqrt{2}}{2}$．
9．已知x2+y2+4z2=1，则x+y+4z的最大值为$\sqrt{6}$．
16．若（1-3x）2015=a0+a1x+…a2015x2015（x∈R），则$\frac{{a}_{1}}{3}+\frac{{a}_{2}}{{3}^{2}}+…\frac{{a}_{2015}}{{3}^{2015}}$的值为（　　）
A．3B．0C．-1D．-3
13．已知i为虚数单位，则i2015=（　　）
A．1B．-2C．iD．-i
14．已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1，（a＞b＞0）的离心率e=$\frac{{\sqrt{6}}}{3}$，直线y=x与椭圆交于A，B两点，C为椭圆的右顶点，$\overrightarrow{OA}•\overrightarrow{OC}=\frac{3}{2}$
（1）求椭圆的方程；
（2）若椭圆上存在两点E，F使$\overrightarrow{OE}+\overrightarrow{OF}=λ\overrightarrow{OA}$，λ∈（0，2），求△OEF面积的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网