题目内容
【题目】已知函数f(x)= ![]() ,点A、B是函数f(x)图象上不同两点,则∠AOB(O为坐标原点)的取值范围是( )
,点A、B是函数f(x)图象上不同两点,则∠AOB(O为坐标原点)的取值范围是( )
A.(0, ![]() )
)
B.(0, ![]() ]
]
C.(0, ![]() )
)
D.(0, ![]() ]
]
【答案】A
【解析】解:当x≤0时,由y= ![]() 得y2﹣9x2=1,(x≤0),此时对应的曲线为双曲线,双曲线的渐近线为y=﹣3x,此时渐近线的斜率k1=﹣3, 当x>0时,f(x)=1+xex﹣1 , 当过原点的直线和f(x)相切时,设切点为(a,1+aea﹣1),
得y2﹣9x2=1,(x≤0),此时对应的曲线为双曲线,双曲线的渐近线为y=﹣3x,此时渐近线的斜率k1=﹣3, 当x>0时,f(x)=1+xex﹣1 , 当过原点的直线和f(x)相切时,设切点为(a,1+aea﹣1),
函数的导数f′(x)=ex﹣1+xex﹣1=(x+1)ex﹣1 ,
则切线斜率k2=f′(a)=(a+1)ea﹣1 ,
则对应的切线方程为y﹣(1+aea﹣1)=(1+a)ea﹣1(x﹣a),
即y=(1+a)ea﹣1(x﹣a)+1+aea﹣1 ,
当x=0,y=0时,(1+a)ea﹣1(﹣a)+1+aea﹣1=0,
即a2ea﹣1+aea﹣1=1+aea﹣1 ,
即a2ea﹣1=1,得a=1,此时切线斜率k2=2,
则切线和y=﹣3x的夹角为θ,
则tanθ=| ![]() |=
|= ![]() ,则θ=
,则θ= ![]() ,
,
故∠AOB(O为坐标原点)的取值范围是(0, ![]() ),
),
故选:A.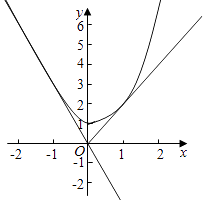

练习册系列答案
相关题目
【题目】某学生对其亲属30人的饮食习惯进行了一次调查,并用下图所示的茎叶图表示30人的饮食指数.(说明:图中饮食指数低于70的人,饮食以蔬菜为主;饮食指数高于70的人,饮食以肉类为主)
(1)根据以上数据完成下面的2×2列联表:
主食 蔬菜 | 主食 肉类 | 总计 | |
50岁以下 | |||
50岁以上 | |||
总计 |
(2)能否在犯错误的概率不超过0.010的前提下认为“其亲属的饮食习惯与年龄有关”?并写出简要分析.
附参考公式:![]()
|
|
|
|
|
|
|
|
|
|
|
|

