题目内容
【题目】设首项为1的正项数列{an}的前n项和为Sn,数列![]() 的前n项和为Tn,且
的前n项和为Tn,且![]() ,其中p为常数.
,其中p为常数.
(1)求p的值;
(2)求证:数列{an}为等比数列;
(3)证明:“数列an,2xan+1,2yan+2成等差数列,其中x、y均为整数”的充要条件是“x=1,且y=2”.
【答案】(1)p=2;(2)见解析(3)见解析
【解析】
(1)取n=1时,由![]() 得p=0或2,计算排除p=0的情况得到答案.
得p=0或2,计算排除p=0的情况得到答案.
(2)![]() ,则
,则![]() ,相减得到3an+1=4﹣Sn+1﹣Sn,再化简得到
,相减得到3an+1=4﹣Sn+1﹣Sn,再化简得到![]() ,得到证明.
,得到证明.
(3)分别证明充分性和必要性,假设an,2xan+1,2yan+2成等差数列,其中x、y均为整数,计算化简得2x﹣2y﹣2=1,设k=x﹣(y﹣2),计算得到k=1,得到答案.
(1)n=1时,由![]() 得p=0或2,若p=0时,
得p=0或2,若p=0时,![]() ,
,
当n=2时,![]() ,解得a2=0或
,解得a2=0或![]() ,
,
而an>0,所以p=0不符合题意,故p=2;
(2)当p=2时,![]() ①,则
①,则![]() ②,
②,
②﹣①并化简得3an+1=4﹣Sn+1﹣Sn③,则3an+2=4﹣Sn+2﹣Sn+1④,
④﹣③得![]() (n∈N*),
(n∈N*),
又因为![]() ,所以数列{an}是等比数列,且
,所以数列{an}是等比数列,且![]() ;
;
(3)充分性:若x=1,y=2,由![]() 知an,2xan+1,2yan+2依次为
知an,2xan+1,2yan+2依次为![]() ,
,![]() ,
,![]() ,
,
满足![]() ,即an,2xan+1,2yan+2成等差数列;
,即an,2xan+1,2yan+2成等差数列;
必要性:假设an,2xan+1,2yan+2成等差数列,其中x、y均为整数,又![]() ,
,
所以![]() ,化简得2x﹣2y﹣2=1,
,化简得2x﹣2y﹣2=1,
显然x>y﹣2,设k=x﹣(y﹣2),
因为x、y均为整数,所以当k≥2时,2x﹣2y﹣2>1或2x﹣2y﹣2<1,
故当k=1,且当x=1,且y﹣2=0时上式成立,即证.

 名校课堂系列答案
名校课堂系列答案【题目】某企业生产的某种产品被检测出其中一项质量指标存在问题. 该企业为了检查生产该产品的甲、乙两条流水线的生产情况,随机地从这两条流水线上生产的大量产品中各抽取![]() 件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在
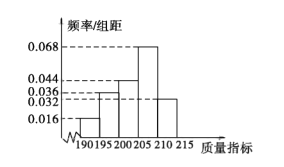
件产品作为样本,测出它们的这一项质量指标值.若该项质量指标值落在![]() 内,则为合格品,否则为不合格品.表 1是甲流水线样本的频数分布表,如图所示是乙流水线样本的频率分布直方图.
内,则为合格品,否则为不合格品.表 1是甲流水线样本的频数分布表,如图所示是乙流水线样本的频率分布直方图.
表1 甲流水线样本的频数分布表
质量指标值 | 频数 |
|
|
|
|
|
|
|
|
|
|
(1)若将频率视为概率,某个月内甲、乙两条流水线均生产了![]() 万件产品,则甲、乙两条流水线分别生产出不合格品约多少件?
万件产品,则甲、乙两条流水线分别生产出不合格品约多少件?
(2)在甲流水线抽取的样本的不合格品中随机抽取两件,求两件不合格品的质量指标值均偏大的概率;
(3)根据已知条件完成下面![]() 列联表,并判断在犯错误概率不超过
列联表,并判断在犯错误概率不超过![]() 的前提下能否认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
的前提下能否认为“该企业生产的这种产品的质量指标值与甲、乙两条流水线的选择有关”?
甲生产线 | 乙生产线 | 合计 | |
合格品 | |||
不合格品 | |||
合计 |
附:![]() (其中
(其中![]() 为样本容量)
为样本容量)
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
【题目】某网络平台从购买该平台某课程的客户中,随机抽取了100位客户的数据,并将这100个数据按学时数,客户性别等进行统计,整理得到如表:
学时数 |
|
|
|
|
|
|
|
男性 | 18 | 12 | 9 | 9 | 6 | 4 | 2 |
女性 | 2 | 4 | 8 | 2 | 7 | 13 | 4 |
(1)根据上表估计男性客户购买该课程学时数的平均值(同一组中的数据用该组区间的中点值作代表,结果保留小数点后两位);
(2)从这100位客户中,对购买该课程学时数在20以下的女性客户按照分层抽样的方式随机抽取7人,再从这7人中随机抽取2人,求这2人购买的学时数都不低于15的概率.
(3)将购买该课程达到25学时及以上者视为“十分爱好该课程者”,25学时以下者视,为“非十分爱好该课程者”.请根据已知条件完成以下![]() 列联表,并判断是否有99.9%的把握认为“十分爱好该课程者”与性别有关?
列联表,并判断是否有99.9%的把握认为“十分爱好该课程者”与性别有关?
非十分爱好该课程者 | 十分爱好该课程者 | 合计 | |
男性 | |||
女性 | |||
合计 | 100 |
附:![]() ,
,![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |