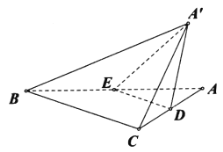
题目内容
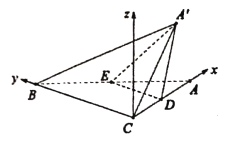
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,现沿
,现沿![]() 的中位线
的中位线![]() 将
将![]() 翻折至
翻折至![]() ,使得二面角
,使得二面角![]() 为
为![]() .
.
(1)求证:![]() ;
;
(2)求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析;(2)![]()
【解析】
(1)由已知可得![]() ,进而证
,进而证![]() 平面
平面![]() ,即可证明结论;
,即可证明结论;
(2)取![]() 中点
中点![]() ,连
,连![]() ,则
,则![]() ,求
,求![]() 与平面
与平面![]() 所成角即可,由(1)得平面
所成角即可,由(1)得平面![]() 平面
平面![]() ,在平面
,在平面![]() 内过
内过![]() 作
作![]() 于
于![]() ,连
,连![]() ,可得
,可得![]() 平面
平面![]() ,
,![]() 为
为![]() 与平面
与平面![]() 所成的角,解
所成的角,解![]() 即可,或建立空间直角坐标系,用向量法求解.
即可,或建立空间直角坐标系,用向量法求解.
(1)因为![]() ,
,![]() ,所以
,所以![]() ,
,![]() ,
,
![]() ,所以
,所以![]() 平面
平面![]() ,
,
![]() 平面
平面![]() ,所以
,所以![]() .
.
(2)解法一:取![]() 中点
中点![]() ,在平面
,在平面![]() 内过
内过![]() 作
作![]() 于
于![]() ,
,
连接![]() ,由(1)可知,
,由(1)可知,![]() 平面
平面![]() ,∴平面
,∴平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,∴
,∴![]() 为
为![]() 与平面
与平面![]() 所成的角,
所成的角,
由(1)可知![]()
![]() 为二面角
为二面角![]() 的平面角,即
的平面角,即![]() ,
,
且![]() ,∴
,∴![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 中,
中,![]() ,
,
在![]() 中,
中,![]() ,
,
∵![]() ,∴直线
,∴直线![]() 与平面
与平面![]() 所成角的正弦值也为
所成角的正弦值也为![]() .
.
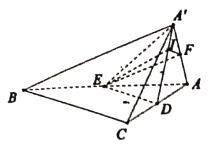
解法二:由(1)得![]() 平面
平面![]() ,因为
,因为![]() ,所以
,所以![]() 平面
平面![]() ,
,
以![]() 为原点,
为原点,![]() ,
,![]() 分别为
分别为![]() ,
,![]() 轴,建立空间直角坐标系,
轴,建立空间直角坐标系,
则![]() ,
,![]() ,
,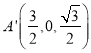 ,
,![]() ,
,
所以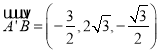 ,
,
设平面![]() 的法向量为
的法向量为![]() ,
,
由 ,即
,即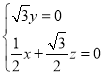 ,
,![]() ,
,
令![]() ,则
,则![]() ,所以
,所以![]() ,
,
设![]() 与平面
与平面![]() 所成角为
所成角为![]() ,
,
则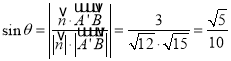 .
.
∴直线![]() 与平面
与平面![]() 所成角的正弦值也为
所成角的正弦值也为![]() .
.

练习册系列答案
相关题目
【题目】某市为了了解该市教师年龄分布情况,对年龄在![]() 内的5000名教师进行了抽样统计,根据分层抽样的结果,统计员制作了如下的统计表格:
内的5000名教师进行了抽样统计,根据分层抽样的结果,统计员制作了如下的统计表格:
年龄区间 |
|
|
|
|
教师人数 | 2000 | 1300 | ||
样本人数 | 130 |
由于不小心,表格中部分数据被污染,看不清了,统计员只记得年龄在![]() 的样本人数比年龄在
的样本人数比年龄在![]() 的样本人数多10,根据以上信息回答下列问题:
的样本人数多10,根据以上信息回答下列问题:

(1)求该市年龄在![]() 的教师人数;
的教师人数;
(2)试根据上表做出该市教师按照年龄的人数频率分布直方图,并求该市教师年龄的平均数![]() 及方差
及方差![]() (同一组的数据用该组区间的中点值作代表).
(同一组的数据用该组区间的中点值作代表).