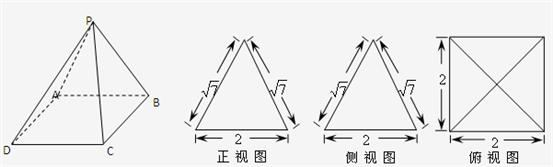
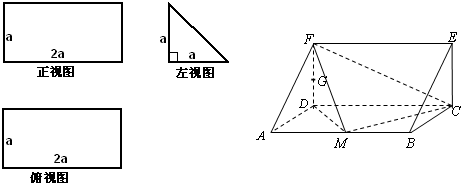
题目内容
一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.
(1)求证:![]()
(2)当FG=GD时,在棱AD上确定一点P,使得GP//平面FMC,并给出证明.
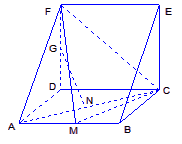

(1)略(2)点P在A点处
解析:
证明:由三视图可得直观图为直三棱柱且底面ADF中AD⊥DF,DF=AD=DC
(1)连接DB,可知B、N、D共线,且AC⊥DN
又FD⊥AD FD⊥CD,
![]() FD⊥面ABCD
FD⊥面ABCD
![]() FD⊥AC
FD⊥AC
![]() AC⊥面FDN
AC⊥面FDN ![]()
![]() GN⊥AC
GN⊥AC
(2)点P在A点处
证明:取DC中点S,连接AS、GS、GA
![]() G是DF的中点,
G是DF的中点,![]() GS//FC,AS//CM
GS//FC,AS//CM
![]() 面GSA//面FMC
面GSA//面FMC
![]()
![]() GA//面FMC 即GP//面FMC
GA//面FMC 即GP//面FMC

练习册系列答案
相关题目
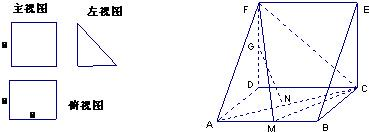 一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.
一个多面体的直观图和三视图如图所示,其中M、N分别是AB、AC的中点,G是DF上的一动点.