题目内容
【题目】如图,在边长为2的正方形ABCD中,E为线段AB的中点,将△ADE沿直线DE翻折成△A′DE,使得平面A′DE⊥平面BCDE,F为线段A′C的中点.
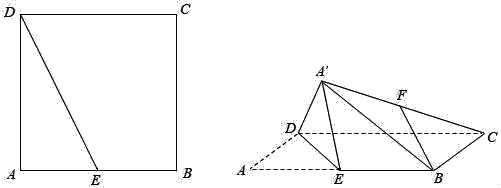
(Ⅰ)求证:BF∥平面A′DE;
(Ⅱ)求直线A′B与平面A′DE所成角的正切值.
【答案】(Ⅰ)详见解析(Ⅱ)![]()
【解析】
(Ⅰ)取A'D的中点M,连接 FM,EM,由已知得四边形BFME为平行四边形,由此能证明BF∥平面A'DE.
(Ⅱ)在平面BCDE内作BN⊥DE,交DE的延长线于点N,则BN⊥平面A'DE,连接A'N,∠BA'N为A'B与平面A'DE所成的角,由此能求出直线A'B与平面A'DE所成角的正切值.
(Ⅰ)证明:取A'D的中点M,连接 FM,EM.
∵F为A'C中点,∴FM∥CD且![]() ,
,
∴BE∥FM且BE=FM,∴四边形BFME为平行四边形,∴BF∥EM,
又EM平面A'DE,BF平面A'DE,
∴BF∥平面A'DE.
(Ⅱ)在平面BCDE内作BN⊥DE,交DE的延长线于点N,
∵平面A'DE⊥平面BCDE,平面A'DE∩平面BCDE=DE,
∴BN⊥平面A'DE,连接A'N,
则∠BA'N为A'B与平面A'DE所成的角,
∵△BNE∽△DAE,BE=1,![]() ,∴
,∴![]() .
.
在△A'DE中作A'P⊥DE垂足为P,∵A'E=1,A'D=2,
∴![]() ,∵
,∵![]() ,∴在直角△A'PN中,
,∴在直角△A'PN中,![]() ,
,
又![]() ,∴
,∴![]() ,
,
∴在直角△A'BN中,![]() ,
,
∴直线A'B与平面A'DE所成角的正切值为![]() .
.

 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案【题目】为了解一家企业生产的某类产品的使用寿命(单位:小时),现从中随机抽取一定数量的产品进行测试,绘制频率分布直方图如图所示.

(1)假设同一组中的每个数据可用该组区间的中点值代替,估算这批产品的平均使用寿命;
(2)已知该企业生产的这类产品有甲、乙两个系列,产品使用寿命不低于60小时为合格,合格产品中不低于90小时为优异,其余为一般.现从合格产品中,用分层抽样的方法抽取70件,其中甲系列有35件(1件优异).请完成下面的列联表,并根据列联表判断能否有![]() 的把握认为产品优异与系列有关?
的把握认为产品优异与系列有关?
甲系列 | 乙系列 | 合计 | |
优异 | |||
一般 | |||
合计 |
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:![]() ,其中
,其中![]() .
.
【题目】已知![]() 三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
三个班共有学生100人,为调查他们的体育锻炼情况,通过分层抽样获取了部分学生一周的锻炼时间,数据如下表(单位:小时).
| 6 |
| 7 | |
| 6 | 7 | 8 | |
| 5 | 6 | 7 | 8 |
(Ⅰ)试估计![]() 班学生人数;
班学生人数;
(Ⅱ)从![]() 班和
班和![]() 班抽出来的学生中各选一名,记
班抽出来的学生中各选一名,记![]() 班选出的学生为甲,
班选出的学生为甲,![]() 班选出的学生为乙,若学生锻炼相互独立,求甲的锻炼时间大于乙的锻炼时间的概率.
班选出的学生为乙,若学生锻炼相互独立,求甲的锻炼时间大于乙的锻炼时间的概率.