题目内容
已知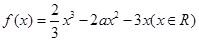 .
.
(Ⅰ)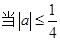 时,求证
时,求证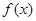 在
在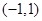 内是减函数;
内是减函数;
(Ⅱ)若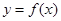 在
在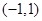 内有且只有一个极值点,求实数
内有且只有一个极值点,求实数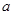 的取值范围.
的取值范围.
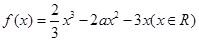 .
.(Ⅰ)
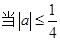 时,求证
时,求证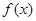 在
在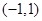 内是减函数;
内是减函数;(Ⅱ)若
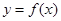 在
在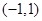 内有且只有一个极值点,求实数
内有且只有一个极值点,求实数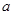 的取值范围.
的取值范围.(1)要证明函数在给定区间的递减的,那恶魔运导数的思想只要证明导数恒大于等于零即可。
(2)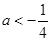 或
或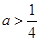 .
.
(2)
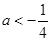 或
或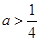 .
. 试题分析:(Ⅰ)∵
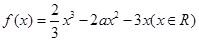
∴
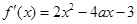 2分
2分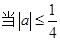 时,有
时,有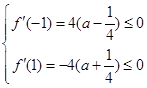 4分
4分又∵二次函数
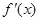 的图象开口向上,
的图象开口向上,∴在
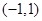 内
内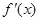 <0,故
<0,故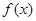 在
在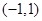 内是减函数. 6分
内是减函数. 6分(Ⅱ)因为
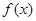 在
在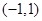 内有且只有一个极值点等价于方程
内有且只有一个极值点等价于方程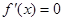 在
在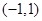 上只有一个解,8分
上只有一个解,8分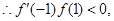 即
即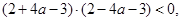 10分
10分就是
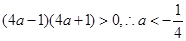 或
或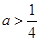 . 12分
. 12分点评:主要是考查了导数在研究函数单调性,以及极值点的运用,属于基础题。

练习册系列答案
 期末集结号系列答案
期末集结号系列答案
相关题目
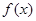 的定义域为R,
的定义域为R,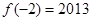 ,对任意
,对任意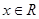 ,都有
,都有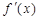 <
<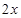 成立,则不等式
成立,则不等式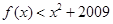 的解集为( )
的解集为( )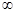 )
)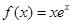 ,则
,则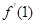 =
= 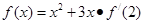 ,则
,则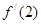 =
= 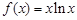 .
. 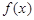 的最小值;
的最小值;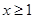 都有
都有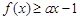 ,求实数
,求实数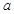 的取值范围.
的取值范围.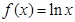 的图像在点
的图像在点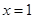 处的切线方程是 .
处的切线方程是 .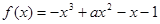 在
在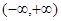 上是单调函数,则实数a的取值范围是( )
上是单调函数,则实数a的取值范围是( )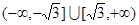
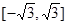
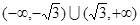
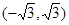
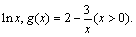
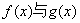 的大小关系;
的大小关系;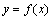 和
和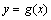 是否存在公切线,若存在,求出公切线方程,若不存在,说明理由;
是否存在公切线,若存在,求出公切线方程,若不存在,说明理由;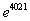 的大小,并写出判断过程.
的大小,并写出判断过程.