题目内容
【题目】已知圆 ![]() 与直线
与直线 ![]() 相切.
相切.
(1)求圆 ![]() 的方程;
的方程;
(2)过点 ![]() 的直线
的直线 ![]() 截圆所得弦长为
截圆所得弦长为 ![]() ,求直线
,求直线 ![]() 的方程;
的方程;
(3)设圆 ![]() 与
与 ![]() 轴的负半轴的交点为
轴的负半轴的交点为 ![]() ,过点
,过点 ![]() 作两条斜率分别为
作两条斜率分别为 ![]() 的直线交圆
的直线交圆 ![]() 于
于 ![]() 两点,且
两点,且 ![]() ,证明:直线
,证明:直线 ![]() 恒过一个定点,并求出该定点坐标.
恒过一个定点,并求出该定点坐标.
【答案】
(1)解:
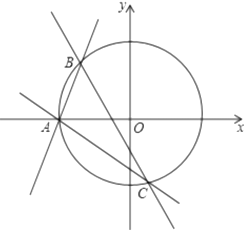
∵圆 ![]() 与直线
与直线 ![]() 相切,
相切,
∴圆心 ![]() 到直线的距离为
到直线的距离为 ![]() ,
,
∴圆 ![]() 的方程为:
的方程为: ![]() .
.
(2)解:若直线 ![]() 的斜率不存在,直线
的斜率不存在,直线 ![]() 为
为 ![]() ,
,
此时直线 ![]() 截圆所得弦长为
截圆所得弦长为 ![]() ,符合题意;
,符合题意;
若直线 ![]() 的斜率存在,设直线
的斜率存在,设直线 ![]() 为
为 ![]() ,即
,即 ![]() ,
,
由题意知,圆心到直线的距离为 ![]() ,解得:
,解得: ![]() ,
,
此时直线 ![]() 为
为 ![]() ,
,
则所求的直线 ![]() 为
为 ![]() 或
或 ![]()
(3)解:由题意知, ![]() ,设直线
,设直线 ![]() ,
,
与圆方程联立得: ![]() ,
,
消去 ![]() 得:
得: ![]() ,
,
∴ ![]()
∴ ![]() ,
, ![]() ,即
,即 ![]() ,
,
∵ ![]() ,用
,用 ![]() 代替
代替 ![]() 得:
得: ![]()
∴直线 ![]() 的方程为:
的方程为: 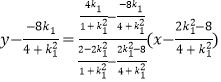
即 ![]()
![]() ,
,
整理得: ![]()
![]()
则直线 ![]() 定点为
定点为 ![]()
【解析】(1)由圆与直线相切得到圆心到切线的距离公式等于圆的半径列出关于r的方程,求出其值即可求出圆的方程。(2)分两种情况:当直线的斜率不存在时直线x=1满足题意;当直线的斜率存在时,设出直线的方程,根据直线与圆的切线得到圆心到直线的距离d=r,列出关于k的方程解出方程求出k的值,进而得到直线的方程,(3)根据题意求出点A的坐标,设出直线AB的方程与圆的方程联立消去y得到关于x的一元二次方程,利用韦达定理表示出两根之积,将A的横坐标代入表示出B的横坐标,进而表示出B的纵坐标确定出B的坐标,由题中 k1 k2 = 2,表示出点C的坐标故可求出直线BC的解析式,进而可得出直线BC恒过一个定点,求出该点坐标即可。
【考点精析】掌握圆的标准方程和直线与圆的三种位置关系是解答本题的根本,需要知道圆的标准方程:![]() ;圆心为A(a,b),半径为r的圆的方程;直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.
;圆心为A(a,b),半径为r的圆的方程;直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点.

 阅读快车系列答案
阅读快车系列答案