题目内容
【题目】已知动点![]() 满足:
满足:![]() .
.
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若点![]() ,
,![]() 分别位于
分别位于![]() 轴与
轴与![]() 轴的正半轴上,直线
轴的正半轴上,直线![]() 与曲线
与曲线![]() 相交于
相交于![]() ,
,![]() 两点,
两点,![]() ,试问在曲线
,试问在曲线![]() 上是否存在点
上是否存在点![]() ,使得四边形
,使得四边形![]() (
(![]() 为坐标原点)为平行四边形?若存在,求出直线
为坐标原点)为平行四边形?若存在,求出直线![]() 的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
【答案】(1)![]() ;(2)不存在.
;(2)不存在.
【解析】
(1)由椭圆的定义可得点![]() 的轨迹为椭圆,且
的轨迹为椭圆,且![]() ,
,![]() ,进而可得其方程;(2)设直线
,进而可得其方程;(2)设直线![]() 的方程为
的方程为![]() ,先根据
,先根据![]() ,可得
,可得![]() ,①,再根据韦达定理,点在椭圆上可得
,①,再根据韦达定理,点在椭圆上可得![]() ,②,将①代入②可得
,②,将①代入②可得![]() ,该方程无解,问题得以解决.
,该方程无解,问题得以解决.
(1)由已知,动点![]() 到点
到点![]() ,
,![]() 的距离之和为4,且
的距离之和为4,且![]() ,
,
所以动点![]() 的轨迹为椭圆,
的轨迹为椭圆,
且![]() ,
,![]() ,所以
,所以![]() ,
,
所以动点![]() 的轨迹
的轨迹![]() 的方程为
的方程为![]() .
.
(2)由题意知![]() 的斜率存在且不为零,
的斜率存在且不为零,
设直线![]() 的方程为
的方程为![]() ,
,
∵![]() ,∴
,∴![]() ,即
,即![]() ,①
,①
联立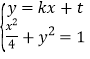 消
消![]() 可得
可得![]() ,
,
设![]() ,
,![]() ,∴
,∴![]() ,
,![]() ,
,
∴![]() ,
,
∵四边形![]() 为平行四边形,故
为平行四边形,故![]() ,
,
∴![]() ,整理可得
,整理可得![]() ,②,
,②,
将①代入②可得![]() ,该方程无解,故这样的直线不存在.
,该方程无解,故这样的直线不存在.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
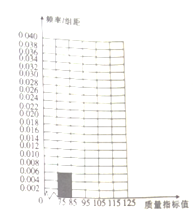
【题目】某种产品的质量以其质量指标值衡量,质量指标值越大表明质量越好,现用一种新配方做试验,生产了100件这种产品,并测量了每件产品的质量指标值,得到下面试验结果:
质量指标值 |
|
|
|
|
|
频数 | 6 | 26 | 38 | 22 | 8 |
(1)将答题卡上列出的这些数据的频率分布表填写完整,并补齐频率分布直方图;
(2)估计这种产品质量指标值的平均值(同一组中的数据用该组区间的中点值作代表)与中位数(结果精确到0.1).
质量指标值分组 | 频数 | 频率 |
| 6 | 0.06 |
| ||
| ||
| ||
| ||
合计 | 100 | 1 |