题目内容
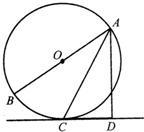如图，已知AB是⊙O的直径，AC为弦，且平分∠BAD，AD⊥CD，垂足为D．（1）求证：CD是⊙O切线；
（2）若⊙O的直径为4，AD=3，求∠BAC的度数．
分析：（1）连接OC，证明∠OCD=90°，得出CD是⊙O切线．
（2）连接BC，证明△BAC∽△CAD，求出AC的长度，再求出∠BAC的余弦，得出∠BAC的度数．
（2）连接BC，证明△BAC∽△CAD，求出AC的长度，再求出∠BAC的余弦，得出∠BAC的度数．
解答：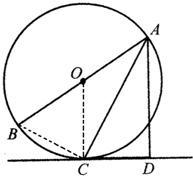
证明：（1）连接OC，
∵OA=OC，
∴∠OCA=∠OAC．
∵AC平分∠BAD，
∴∠BAC=∠CAD．
∴∠OCA=∠CAD．
∴OC∥AD．
又∵AD⊥CD，
∴OC⊥CD．
∴OC是⊙O的切线．
（2）连接BC，
∵AB是直径，
∴∠BCA=90°．
∴∠BCA=∠ADC=90°．
∵∠BAC∠=∠CAD，
∴△BAC∽△CAD．
∴
=
即
=
．
∴AC=2
．
在Rt△ABC中，cos∠BAC=
=
．
∴∠BAC=30°．
证明：（1）连接OC，∵OA=OC，
∴∠OCA=∠OAC．
∵AC平分∠BAD，
∴∠BAC=∠CAD．
∴∠OCA=∠CAD．
∴OC∥AD．
又∵AD⊥CD，
∴OC⊥CD．
∴OC是⊙O的切线．
（2）连接BC，
∵AB是直径，
∴∠BCA=90°．
∴∠BCA=∠ADC=90°．
∵∠BAC∠=∠CAD，
∴△BAC∽△CAD．
∴
| AB |
| AC |
| AC |
| AD |
| 4 |
| AC |
| AC |
| 3 |
∴AC=2
| 3 |
在Rt△ABC中，cos∠BAC=
| AC |
| AB |
| ||
| 2 |
∴∠BAC=30°．
点评：本题主要考查了圆的切线的判定定理的证明．连接半径是证明切线的一种常用辅助线的做法，求角的度数可以借助于三角函数．
练习册系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目
选做题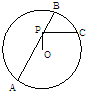
如图，已知AB是⊙O的一条弦，点P为AB上一点，PC⊥OP，PC交⊙O于C，若AP=4，PB=2，则PC的长是（ ）
如图，已知AB是⊙O的直径，点C是⊙O上的动点（异于A、B），过动点C的直线VC垂直于⊙O所在的平面，D，E分别是VA，VC的中点．
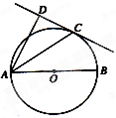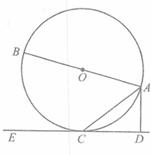
如图，已知AB是⊙O的直径，直线CD与⊙O相切于点C，AC平分∠DAB．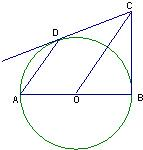
如图，已知AB是⊙O的直径，BC是⊙O的切线，切点为B，OC平行于弦AD，OA=2．