题目内容
若不等式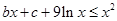 对任意的
对任意的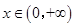 ,
,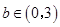 恒成立,则实数
恒成立,则实数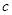 的取值范围是 .
的取值范围是 .
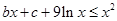 对任意的
对任意的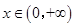 ,
,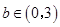 恒成立,则实数
恒成立,则实数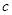 的取值范围是 .
的取值范围是 . 
试题分析:根据题意,得关于b的函数:
 ,这是一个一次函数,要使
,这是一个一次函数,要使 对任意的
对任意的 恒成立,则:
恒成立,则: ,即有:
,即有: 对任意的
对任意的 恒成立,则有:
恒成立,则有: ,可令函数
,可令函数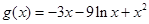 ,求导可得:
,求导可得: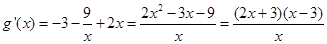 ,发现有:
,发现有: ,故有:
,故有: .
.
练习册系列答案
相关题目
题目内容
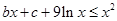 对任意的
对任意的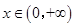 ,
,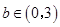 恒成立,则实数
恒成立,则实数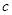 的取值范围是 .
的取值范围是 . 
 ,这是一个一次函数,要使
,这是一个一次函数,要使 对任意的
对任意的 恒成立,则:
恒成立,则: ,即有:
,即有: 对任意的
对任意的 恒成立,则有:
恒成立,则有: ,可令函数
,可令函数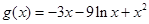 ,求导可得:
,求导可得: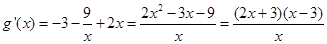 ,发现有:
,发现有: ,故有:
,故有: .
.